2016-2017学年山东省临沂市蒙阴县九年级上学期期末数学试卷

试卷更新日期：2017-04-10 类型：期末考试

进入出卷网下载

一、选择题：相信你一定能选对！

1. 下列的平面几何图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列命题中，是真命题的为（）

A、锐角三角形都相似 B、直角三角形都相似 C、等腰三角形都相似 D、等边三角形都相似

查看试题解析
3. 从下列直角三角板与圆弧的位置关系中，可判断圆弧为半圆的是（）

A、 B、 C、 D、

查看试题解析
4. 一个不透明的盒子中装有2个红球和1个白球，它们除颜色外都相同．若从中任意摸出一个球，则下列叙述正确的是（）

A、摸到红球是必然事件 B、摸到白球是不可能事件 C、摸到红球比摸到白球的可能性相等 D、摸到红球比摸到白球的可能性大

查看试题解析
5. 圆内接四边形ABCD中，已知∠A=70°，则∠C=（）

A、20° B、30° C、70° D、110°

查看试题解析
6. 若关于x的方程2x²﹣ax+a﹣2=0有两个相等的实根，则a的值是（）

A、﹣4 B、4 C、4或﹣4 D、2

查看试题解析
7. 在平面直角坐标系中，点A的坐标为（﹣1，﹣2），将OA绕原点O逆时针旋转180°得到OA′，点A′的坐标为（a，b），则a﹣b等于（）

A、1 B、﹣1 C、3 D、﹣3

查看试题解析
8. 抛物线y=﹣x²+bx+c上部分点的横坐标x，纵坐标y的对应值如表：
x
…
﹣2
﹣1
0
1
2
…
y
…
0
4
6
6
4
…
从上表可知，有下列说法：
①抛物线与y轴的交点为（0，6）；
②抛物线的对称轴是x=1；
③抛物线与x轴有两个交点，它们之间的距离是 $\frac{5}{2}$ ；
④在对称轴左侧y随x增大而增大．
其中正确的说法是（）

A、①②③ B、②③④ C、②③ D、①④

查看试题解析
9. 如图，在平面直角坐标系中，点A，B，C的坐标为（1，4），（5，4），（1，﹣2），则△ABC外接圆的圆心坐标是（）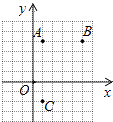

A、（2，3） B、（3，2） C、（1，3） D、（3，1）

查看试题解析
10. 如图，直线 $y = \frac{3}{4} x$ 与双曲线 $y = \frac{k}{x} (x > 0)$ 交于点A．将直线 $y = \frac{3}{4} x$ 向右平移6个单位后，与双曲线 $y = \frac{k}{x} (x > 0)$ 交于点B，与x轴交于点C，若 $\frac{A O}{B C} = 2$ ，则k的值为（）

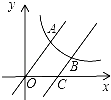A、12 B、14 C、18 D、24

查看试题解析

二、填空题。

11. 已知正六边形的半径是2，则这个正六边形的边长是

查看试题解析
12. 如图，点D是等边△ABC内的一点，如果△ABD绕点A逆时针旋转后能与△ACE重合，那么旋转了度．

查看试题解析
13. 如图，在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°，得到Rt△EFC，若AB= $\sqrt{5}$ ，BC=1，则阴影部分的面积为．

查看试题解析
14. 小勇第一次抛一枚质地均匀的硬币时正面向上，他第二次再抛这枚硬币时，正面向上的概率是．

查看试题解析
15. 一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是

查看试题解析
16. 如图，AB是⊙O的直径，AB=2，点C在⊙O上，∠CAB=30°，D为 $\overset{⌢}{B C}$ 的中点，P是直径AB上一动点，则PC+PD的最小值为．

查看试题解析
17. 如图是反比例函数y= $\frac{k}{x}$ 在第二象限内的图象，若图中的矩形OABC的面积为2，则k=

查看试题解析
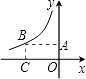18. 如图，Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=4cm，D为BC的中点，若动点E以1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E点的运动时间为t秒（0≤t＜12），连接DE，当△BDE是直角三角形时，t的值为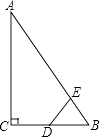

查看试题解析

三、解答题。

19. 解下列方程

(1)、x²+x﹣1=0

(2)、x（x﹣2）+x﹣2=0．

查看试题解析
20.
如图，若将△ABC绕点C逆时针旋转90°后得到△A′B′C′，

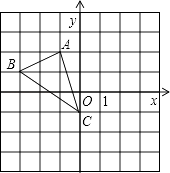(1)、在图中画出△A′B′C′；

(2)、求出点A经过的路径长．

查看试题解析
21. 如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点M，MN⊥AC于点N．
求证：MN是⊙O的切线．

查看试题解析
22. 如图，在△ABC中，AB=AC，点D、E分别在BC、AB上，且∠BDE=∠CAD．求证：△ADE∽△ABD．

查看试题解析
23. 如图，直线y=x﹣1与反比例函数y= $\frac{k}{x}$ 的图象交于A、B两点，与x轴交于点C，已知点A的坐标为（﹣1，m）．

(1)、求反比例函数的解析式；

(2)、若点P（n，﹣1）是反比例函数图象上一点，过点P作PE⊥x轴于点E，延长EP交直线AB于点F，求△CEF的面积．

查看试题解析
24. 暑假期间，某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面．已知这个矩形操场地面的长为100m，宽为80m，图案设计如图所示：操场的四角为小正方形，阴影部分为四个矩形，四个矩形的宽都为小正方形的边长，在实际铺设的过程总，阴影部分铺红色地面砖，其余部分铺灰色地面砖．

(1)、如果操场上铺灰色地面砖的面积是铺红色地面砖面积的4倍，那么操场四角的每个小正方形边长是多少米？

(2)、如果灰色地面砖的价格为每平方米30元，红色地面砖的价格为每平方米20元，学校现有15万元资金，问这些资金是否能购买所需的全部地面砖？如果能购买所学的全部地面砖，则剩余资金是多少元？如果不能购买所需的全部地面砖，教育局还应该至少给学校解决多少资金？

查看试题解析
25.
如图，已知抛物线y=﹣ $\frac{1}{4}$ x²+bx+4与x轴相交于A、B两点，与y轴相交于点C，若已知A点的坐标为A（﹣2，0）．

(1)、求抛物线的解析式及它的对称轴方程；

(2)、求点C的坐标，连接AC、BC并求线段BC所在直线的解析式；

(3)、试判断△AOC与△COB是否相似？并说明理由．

查看试题解析

x	…	﹣2	﹣1	0	1	2	…
y	…	0	4	6	6	4	…