2016-2017学年江西省宜春市九年级上学期期末数学试卷
试卷更新日期：2017-04-10 类型：期末考试
一、选择题
-
1. 下列图形中，是中心对称图形的是（ ）A、
B、
C、
D、
2. 抛物线y=（x﹣2016）2+2017的顶点坐标是（ ）A、（2016，﹣2017） B、（﹣2016，2017） C、（2016，2017） D、（﹣2016，﹣2017）3. 下列诗句所描述的事件中，是不可能事件的是（ ）A、黄河入海流 B、锄禾日当午 C、大漠孤烟直 D、手可摘星辰4. 要做一顶母线长为20cm，底面半径为10cm的纸质圆锥形圣诞帽，至少需要纸的面积为（ ）A、300πcm2 B、250πcm2 C、200πcm2 D、150πcm25. Rt△ABC中，∠C=90°，AC=8cm，BC=6cm，以点C为圆心5cm为半径的圆与直线AB的位置关系是（ ）A、相交 B、相切 C、相离 D、无法确定6. 二次函数y=ax2+b与反比例函数y= 在同一平面直角坐标系中的图象可能是（ ）A、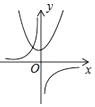
B、
C、
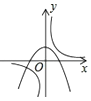D、
二、填空题
-
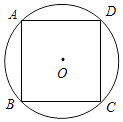
7. 已知点A（9，a）和点B（b，﹣2）关于原点对称，则ba= ．8. 设一元二次方程x2﹣3x﹣1=0的两根为m，n，则mn=9. 在一个不透明的布袋中，红色、黑色、白色的玻璃球共有20个，除颜色外其他完全相同．小明通过多次摸球试验后发现其中摸到红色、黑色球的频率分别稳定在15%和45%，则口袋中白色球很可能有 个．10. 将抛物线y=x2﹣4x+1向左平移2个单位，再向上平移3个单位所得抛物线解析式为 ．11. 如图，正方形ABCD内接于⊙O，弦BC所对的圆周角的度数为 ．
12. 二次函数y=ax2+bx+c（a≠0）的图象如图（虚线部分为对称轴），给出以下5个结论：①x≤1时，y随x的增大而增大；②abc＞0；③b＜a+c；④4a+2b+c＞0；⑤3a﹣b＜0，其中正确的结论有（填上所有正确结论的序号）．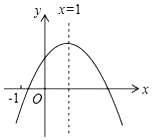
三、解答题。
-
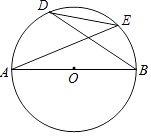
13. 解方程：4（x﹣1）=x（x﹣1）14. 如图，AB是⊙O的直径， = ，且AB=5，BD=4，求弦DE的长．
15. 如图，一次函数y1=x+1的图象与反比例函数y2= （k为常数，且k≠0）的图象都经过点A（m，2），求反比例函数的解析式，并根据图象比较y1和y2的大小（x＞0）．
16. 如图，在边长为1的正方形网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．将△AOB绕点O逆时针旋转90°后得到△A1OB1 ．
(1)、画出旋转后的△A1OB1 ， 点A1的坐标为；(2)、在旋转过程中，点B经过的路径为 ，求 的长．17. 已知关于x的方程x2+ax+a﹣2=0．(1)、求证：不论a取何实数，该方程都有两个不相等的实数根；(2)、若该方程有一根是﹣2，求另一根．18. 已知△ABC内接于⊙O，请仅用无刻度的直尺，根据下列条件分别在图1，图2中画出∠BAC的平分线（保留作图痕迹，不写作法）．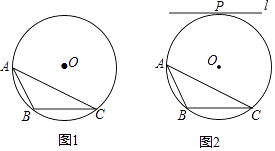
(1)、如图1，P是BC边的中点；(2)、如图2，直线l与⊙O相切于点P，且l∥BC．19. 小源的父母决定中考之后带她去旅游，初步商量有意向的四个景点分别为：A．明月山，B．庐山，C．婺源，D．三清山．由于受到时间限制，只能选两个景点，于是小源的父母决定通过抽签选择，用四张小纸条分别写上四个景点做成四个签（外表无任何不同），让小源随机抽两次，每次抽一个签，每个签抽到的机会相等．(1)、小源最希望去婺源，则小源第一次恰好抽到婺源的概率是多少；(2)、除婺源外，小源还希望去明月山，求小源抽到婺源、明月山两个景点中至少一个的概率是多少．（通过“画树状图”或“列表”进行分析）20. 如图，点B、C、D都在半径为4的⊙O上，过点C作AC∥BD交OB的延长线于点A，连接CD，已知∠CDB=∠OBD=30°．
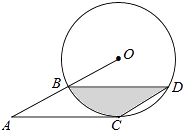(1)、求证：AC是⊙O的切线；(2)、求弦BD的长．21. 寒假里，小斌与爸爸一起销售一种农产品体验生活．已知这种农产品的成本价为每千克20元，根据爸爸的经验，该农产品每天的销售量y（千克）与销售价x（元/千克）有如下关系：y=﹣2x+80．设该农产品每天的销售利润为w元．(1)、求w与x之间的函数关系式；(2)、爸爸说：“物价部门规定这种农产品的销售价不得高于每千克28元”，爸爸想要每天获得150元的销售利润，销售价应定为每千克多少元．22. 冬天来了，晒衣服成了头疼的事情，聪明的小华想到一个好办法，在家后院地面（BD）上立两根等长的立柱AB、CD（均与地面垂直），并在立柱之间悬挂一根绳子．由于挂的衣服比较多，绳子的形状近似成了抛物线y=ax2﹣0.8x+c，如图1，已知立柱AB=CD=2.6米，BD=8米．
(1)、求绳子最低点离地面的距离；(2)、为了防止衣服碰到地面，小华在离AB为3米的位置处用一根垂直于地面的立柱MN撑起绳子（如图2），使左边抛物线F1的最低点距MN为1米，离地面1.6米，求MN的长．23. 已知∠α的顶点在正n边形的中心点O处，∠α绕着顶点O旋转，角的两边与正n边 形的两边分别交于点M、N，∠α与正n边形重叠部分面积为S．(1)、当n=4，边长为2，∠α=90°时，如图（1），请直接写出S的值；
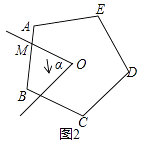
(2)、当n=5，∠α=72°时，如图（2），请问在旋转过程中，S是否发生变化？并说明理由；
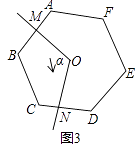
(3)、当n=6，∠α=120°时，如图（3），请猜想S是原正六边形面积的几分之几（不必说明理由）．若∠α的平分线与BC边交于点P，判断四边形OMPN的形状，并说明理由．
24. 已知抛物线y=ax2﹣4ax+b与x轴的一个交点A的坐标为（3，0），与y轴交于点C．(1)、求抛物线与x轴的另一个交点B的坐标；(2)、当a=﹣1时，将抛物线向上平移m个单位后经过点（5，﹣7）．①求m的值及平移前、后抛物线的顶点P、Q的坐标．
②设平移后抛物线与y轴交于点D，问：在平移后的抛物线上是否存在点E，使得△ECD的面积是△EPQ的3倍？若存在，请求出点E的坐标；若不存在，请说明理由．