2017年江西省赣州市石城县中考数学一模试卷
试卷更新日期:2017-04-10 类型:中考模拟
一、选择题
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、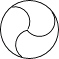 C、
C、 D、
D、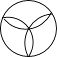 2. 下列运算中,正确的是( )A、m2×m3=m6 B、(m3)2=m5 C、m+m2=2m3 D、﹣m3÷m2=﹣m3. 已知m,n是一元二次方程x2﹣4x﹣3=0的两个实数根,则代数式(m+1)(n+1)的值为( )A、﹣6 B、﹣2 C、0 D、24. 如图是一个底面为正方形的几何体的实物图,则其俯视图为( )
2. 下列运算中,正确的是( )A、m2×m3=m6 B、(m3)2=m5 C、m+m2=2m3 D、﹣m3÷m2=﹣m3. 已知m,n是一元二次方程x2﹣4x﹣3=0的两个实数根,则代数式(m+1)(n+1)的值为( )A、﹣6 B、﹣2 C、0 D、24. 如图是一个底面为正方形的几何体的实物图,则其俯视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC= ,则四边形MABN的面积是( )
5. 如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC= ,则四边形MABN的面积是( )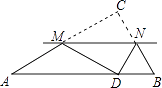 A、 B、 C、 D、6. 已知二次函数y=ax2+bx+c(a≠0)与x轴交于点(x1 , 0)与(x2 , 0),其中x1<x2 , 方程ax2+bx+c﹣a=0的两根为m、n(m<n),则下列判断正确的是( )A、m<n<x1<x2 B、m<x1<x2<n C、x1+x2>m+n D、b2﹣4ac≥0
A、 B、 C、 D、6. 已知二次函数y=ax2+bx+c(a≠0)与x轴交于点(x1 , 0)与(x2 , 0),其中x1<x2 , 方程ax2+bx+c﹣a=0的两根为m、n(m<n),则下列判断正确的是( )A、m<n<x1<x2 B、m<x1<x2<n C、x1+x2>m+n D、b2﹣4ac≥0二、填空题
-
7. 当分式 的值为0时,x的值是 .8. 已知a+b=8,a﹣b=4,则a2﹣b2= .9. 如图,已知二次函数y=x2+bx+c的图像的对称轴是直线x=1,过抛物线上两点的直线AB平行于x轴,若点A的坐标为(0, ),则点B的坐标为 .
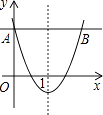 10. 如图,在半径为5的⊙O中,弦AB=6,点C是优弧 上一点(不与A,B重合),则cosC的值为 .
10. 如图,在半径为5的⊙O中,弦AB=6,点C是优弧 上一点(不与A,B重合),则cosC的值为 .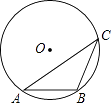 11. 如图,正方体的棱长为a,沿着共一个顶点的三个正方形的对角线裁截掉一个几何体之后,截面△ABC的面积= .
11. 如图,正方体的棱长为a,沿着共一个顶点的三个正方形的对角线裁截掉一个几何体之后,截面△ABC的面积= .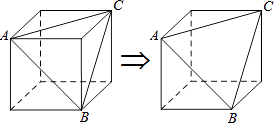 12. 以线段AC为对角线的四边形ABCD(它的四个顶点A、B、C、D按顺时针方向排列),已知AB=BC=CD,∠ABC=100°,∠CAD=40°;则∠BCD的大小为 .
12. 以线段AC为对角线的四边形ABCD(它的四个顶点A、B、C、D按顺时针方向排列),已知AB=BC=CD,∠ABC=100°,∠CAD=40°;则∠BCD的大小为 .三、解答题
-
13. 根据题意解答(1)、计算:|﹣ |+(π﹣3)0+( )﹣1﹣2cos45°(2)、若关于x的一元二次方程x2+(k+3)x+k=0的一个根是﹣2,求方程的另一个根.14. 四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
 (1)、求证:△ADE≌△ABF;(2)、若BC=8,DE=6,求△AEF的面积.15. 如图,在3×3的方阵图中,填写了一些数和代数式(其中每个代数式都表示一个数),使得每行的3个数、每列的3个数、斜对角的3个数之和均相等.
(1)、求证:△ADE≌△ABF;(2)、若BC=8,DE=6,求△AEF的面积.15. 如图,在3×3的方阵图中,填写了一些数和代数式(其中每个代数式都表示一个数),使得每行的3个数、每列的3个数、斜对角的3个数之和均相等.3
4
x
﹣2
y
a
2y﹣x
c
b
备用图
3
4
﹣2
(1)、求x,y的值;(2)、在备用图中完成此方阵图.
16. 如图,由6个形状、大小完全相同的小矩形组成大矩形网格,小矩形的顶点称为这个矩形网格的格点,请仅用无刻度直尺在矩形中完成下列画图.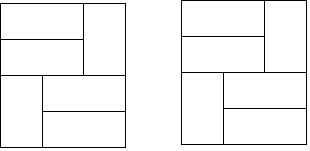 (1)、在图1中画出一个顶点均在格点上的非特殊的平行四边形;(2)、在图2中画出一个顶点均在格点上的正方形.17. 小明家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小明按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.(1)、若小明任意按下一个开关,则下列说法正确的是( )A、小明打开的一定是楼梯灯; B、小明打开的可能是卧室灯; C、小明打开的不可能是客厅灯; D、小明打开走廊灯的概率是(2)、若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图法或列表法加以说明.
(1)、在图1中画出一个顶点均在格点上的非特殊的平行四边形;(2)、在图2中画出一个顶点均在格点上的正方形.17. 小明家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小明按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.(1)、若小明任意按下一个开关,则下列说法正确的是( )A、小明打开的一定是楼梯灯; B、小明打开的可能是卧室灯; C、小明打开的不可能是客厅灯; D、小明打开走廊灯的概率是(2)、若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图法或列表法加以说明. 18.
18.反比例函数y= (x>0)的图像经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB= ,将线段AB沿x轴正方向平移到线段DC的位置,反比例函数y= (x>0)的图像恰好经过DC的中点E.
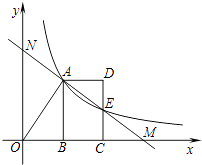 (1)、求k的值和直线AE的函数表达式;(2)、若直线AE与x轴交于点M、与y轴交于点N,请你探索线段AN与线段ME的大小关系,写出你的结论并说明理由.19. 某地区为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费.为更好地决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如下不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
(1)、求k的值和直线AE的函数表达式;(2)、若直线AE与x轴交于点M、与y轴交于点N,请你探索线段AN与线段ME的大小关系,写出你的结论并说明理由.19. 某地区为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费.为更好地决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如下不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题: (1)、此次调查抽取了多少用户的用水量数据?(2)、补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数;(3)、如果自来水公司将基本用水量定为每户25吨,那么该地区20万用户中约有多少用户的用水全部享受基本价格?20. 图1是安装在斜屋面上的热水器,图2是安装该热水器的侧面示意图.已知,斜屋面的倾斜角为25°,长为2.1米的真空管AB与水平线AD的夹角为40°,安装热水器的铁架水平横管BC长0.2米,求
(1)、此次调查抽取了多少用户的用水量数据?(2)、补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数;(3)、如果自来水公司将基本用水量定为每户25吨,那么该地区20万用户中约有多少用户的用水全部享受基本价格?20. 图1是安装在斜屋面上的热水器,图2是安装该热水器的侧面示意图.已知,斜屋面的倾斜角为25°,长为2.1米的真空管AB与水平线AD的夹角为40°,安装热水器的铁架水平横管BC长0.2米,求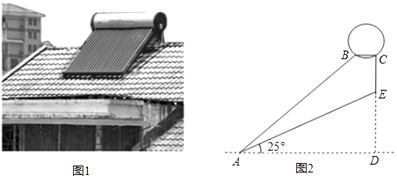 (1)、真空管上端B到AD的距离(结果精确到0.01米);(2)、铁架垂直管CE的长(结果精确到0.01米).21. 在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.
(1)、真空管上端B到AD的距离(结果精确到0.01米);(2)、铁架垂直管CE的长(结果精确到0.01米).21. 在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB. (1)、当OC∥AB时,∠BOC的度数为;(2)、连接AC,BC,当点C在⊙O上运动到什么位置时,△ABC的面积最大?并求出△ABC的面积的最大值;(3)、连接AD,当OC∥AD时,①求出点C的坐标;②直线BC是否为⊙O的切线?请作出判断,并说明理由.22. 探究与应用.试完成下列问题:(1)、如图①,已知等腰Rt△ABC中,∠C=90°,点O为AB的中点,作∠POQ=90°,分别交AC、BC于点P、Q,连结PQ、CO,求证:AP2+BQ2=PQ2;
(1)、当OC∥AB时,∠BOC的度数为;(2)、连接AC,BC,当点C在⊙O上运动到什么位置时,△ABC的面积最大?并求出△ABC的面积的最大值;(3)、连接AD,当OC∥AD时,①求出点C的坐标;②直线BC是否为⊙O的切线?请作出判断,并说明理由.22. 探究与应用.试完成下列问题:(1)、如图①,已知等腰Rt△ABC中,∠C=90°,点O为AB的中点,作∠POQ=90°,分别交AC、BC于点P、Q,连结PQ、CO,求证:AP2+BQ2=PQ2;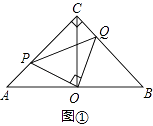 (2)、如图②,将等腰Rt△ABC改为任意直角三角形,点O仍为AB的中点,∠POQ=90°,试探索上述结论AP2+BQ2=PQ2是否仍成立;
(2)、如图②,将等腰Rt△ABC改为任意直角三角形,点O仍为AB的中点,∠POQ=90°,试探索上述结论AP2+BQ2=PQ2是否仍成立; (3)、通过上述探究(可直接运用上述结论),试解决下面的问题:如图③,已知Rt△ABC中,∠C=90°,AC=6,BC=8,点O为AB的中点,过C、O两点的圆分别交AC、BC于P、Q,连结PQ,求△PCQ面积的最大值.
(3)、通过上述探究(可直接运用上述结论),试解决下面的问题:如图③,已知Rt△ABC中,∠C=90°,AC=6,BC=8,点O为AB的中点,过C、O两点的圆分别交AC、BC于P、Q,连结PQ,求△PCQ面积的最大值. 23. 对于二次函数y=x2﹣3x+2和一次函数y=﹣2x+4,把y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图像记作抛物线E,现有点A(2,0)和抛物线E上的点B(﹣1,n),请完成下列任务;(1)、【尝试】①当t=2时,抛物线y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)的顶点坐标为(2)、②判断点A是否在抛物线E上;(3)、③求n的值.(4)、【发现】通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线E总过定点,坐标为 .(5)、
23. 对于二次函数y=x2﹣3x+2和一次函数y=﹣2x+4,把y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图像记作抛物线E,现有点A(2,0)和抛物线E上的点B(﹣1,n),请完成下列任务;(1)、【尝试】①当t=2时,抛物线y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)的顶点坐标为(2)、②判断点A是否在抛物线E上;(3)、③求n的值.(4)、【发现】通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线E总过定点,坐标为 .(5)、【应用】
①二次函数y=﹣3x2+5x+2是二次函数y=x2﹣3x+3和一次函数y=﹣2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由;
②以AB为边作矩形ABCD,使得其中一个顶点落在y轴上;若抛物线E经过A,B,C,D其中的三点,求出所有符合条件的t的值.
