广西贵港市港南区2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-01-09 类型:期中考试
一、选择题
-
1. cos30°的相反数是( )A、
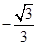 B、
B、 C、
C、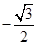 D、
D、 2. 下列函数关系式中属于反比例函数的是( )A、 B、
2. 下列函数关系式中属于反比例函数的是( )A、 B、 C、
C、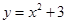 D、
D、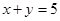 3. 下列图形一定是相似图形的是( )A、两个矩形 B、两个正方形 C、两个直角三角形 D、两个等腰三角形4. 如果α是锐角,且sinα= ,那么cos(90°-α)的值为( )A、 B、
3. 下列图形一定是相似图形的是( )A、两个矩形 B、两个正方形 C、两个直角三角形 D、两个等腰三角形4. 如果α是锐角,且sinα= ,那么cos(90°-α)的值为( )A、 B、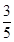 C、
D、
5. 方程2(2x+1)(x-3)=0的两根分别为( )A、 和3 B、
C、
D、
5. 方程2(2x+1)(x-3)=0的两根分别为( )A、 和3 B、 和3
C、 和
D、
和3
C、 和
D、 和
6. 在Rt△ABC中,如果各边长度都扩大3倍,则锐角A的正切值( )A、扩大2倍 B、 缩小为原来的 C、扩大4倍 D、没有变化7. 反比例函数y= 图象上有三个点(-2,y1),(-1,y2),(1,y3),则y1 , y2 , y3的大小关系是( )A、
和
6. 在Rt△ABC中,如果各边长度都扩大3倍,则锐角A的正切值( )A、扩大2倍 B、 缩小为原来的 C、扩大4倍 D、没有变化7. 反比例函数y= 图象上有三个点(-2,y1),(-1,y2),(1,y3),则y1 , y2 , y3的大小关系是( )A、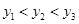 B、
B、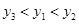 C、
C、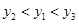 D、
D、 8. 已知直线y=kx(k>0)与双曲线y= 交于点A(x1 , y1),B(x2 , y2)两点,则x1y2+x2y1的值为( )A、 B、
8. 已知直线y=kx(k>0)与双曲线y= 交于点A(x1 , y1),B(x2 , y2)两点,则x1y2+x2y1的值为( )A、 B、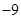 C、0
D、9
9. 如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为 ,把△ABO缩小,则点A的对应点A′的坐标是( )
C、0
D、9
9. 如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为 ,把△ABO缩小,则点A的对应点A′的坐标是( ) A、
A、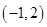 B、
B、 C、
C、 或
或  D、
D、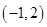 或
或 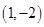 10. 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )
10. 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )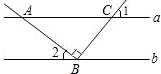 A、
A、 B、
B、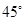 C、
C、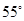 D、
D、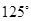 11. 如图,AD∥BE∥CF,直线l1 , l2与这三条平行线分别交于A,B,C和点D,E,F.若AB=2,BC=4,DE=3,则EF的长为( )
11. 如图,AD∥BE∥CF,直线l1 , l2与这三条平行线分别交于A,B,C和点D,E,F.若AB=2,BC=4,DE=3,则EF的长为( )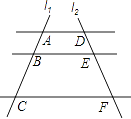 A、5 B、6 C、7 D、912. 如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论的个数为( )
A、5 B、6 C、7 D、912. 如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则以下四个结论中正确结论的个数为( )①OH= BF;②∠CHF=45°;③GH= BC;④DH2=HE•HB.
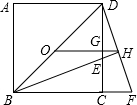 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
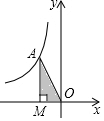
13. 若函数y=(m-1) 是反比例函数,则m= .14. 已知m,n是方程2x2-3x+1=0的两根,则 + = .15. 已知 = = ,则 = .16. 如图,若点A在反比例函数y= (k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为5,则k= .
 17. 如图,△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=2,AD=1,则DB= .
17. 如图,△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=2,AD=1,则DB= .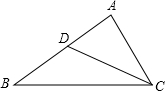 18. 如图△ABC中,边BC=12cm,高AD=6cm,边长为x的正方形PQMN的一边在BC上,其余两个顶点分别在AB、AC上,则正方形的边长x=cm.
18. 如图△ABC中,边BC=12cm,高AD=6cm,边长为x的正方形PQMN的一边在BC上,其余两个顶点分别在AB、AC上,则正方形的边长x=cm.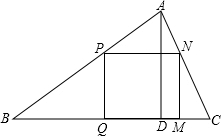
三、计算题
-
19.(1)、计算:20180-| |+( )-1+2cos45°(2)、解方程:3(x+2)2=x2-420. 先化简,再求值:(1- )÷ ,其中a=2sin45°-1.
四、解答题
-
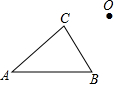
21. 作图:如图所示,O为△ABC外一点,以O为位似中心,将△ABC缩小为原图的 .(只作图,不写作法和步骤)
 22. 已知关于x的方程x2+2x+a-2=0.(1)、若该方程有两个不相等的实数根,求实数a的取值范围;(2)、当该方程的一个根为1时,求a的值及方程的另一根.23. 将进货单价为40元的商品按50元售出时,能卖出500个,已知这种商品每涨价2元,其销售量就减少20个,为了赚得8000元的利润,售价应定为多少?这种货要进多少?24. 某建筑物的金属支架如图所示,根据要求AB长为4m,C为AB的中点,点B到D的距离比立柱CD的长小0.5m,∠BCD=60°,求立柱CD长.
22. 已知关于x的方程x2+2x+a-2=0.(1)、若该方程有两个不相等的实数根,求实数a的取值范围;(2)、当该方程的一个根为1时,求a的值及方程的另一根.23. 将进货单价为40元的商品按50元售出时,能卖出500个,已知这种商品每涨价2元,其销售量就减少20个,为了赚得8000元的利润,售价应定为多少?这种货要进多少?24. 某建筑物的金属支架如图所示,根据要求AB长为4m,C为AB的中点,点B到D的距离比立柱CD的长小0.5m,∠BCD=60°,求立柱CD长.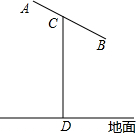 25. 如图,反比例函数y= 的图象与一次函数y=ax﹢b的图象交于C(4,-3),E(-3,4)两点.且一次函数图象交y轴于点A.
25. 如图,反比例函数y= 的图象与一次函数y=ax﹢b的图象交于C(4,-3),E(-3,4)两点.且一次函数图象交y轴于点A.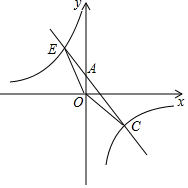 (1)、求反比例函数与一次函数的解析式;(2)、求△COE的面积;(3)、点M在x轴上移动,是否存在点M使△OCM为等腰三角形?若存在,请你直接写出M点的坐标;若不存在,请说明理由.26. 如图
(1)、求反比例函数与一次函数的解析式;(2)、求△COE的面积;(3)、点M在x轴上移动,是否存在点M使△OCM为等腰三角形?若存在,请你直接写出M点的坐标;若不存在,请说明理由.26. 如图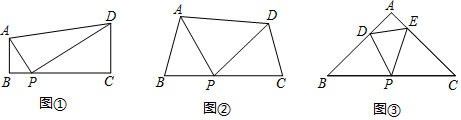 (1)、感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)(2)、探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.(3)、拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=4 ,CE=3,则DE的长为 .
(1)、感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)(2)、探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.(3)、拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=4 ,CE=3,则DE的长为 .