广东省深圳市大鹏新区2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期:2019-01-09 类型:期中考试
一、选择题
-
1. 下列各数中是无理数的是( )A、1 B、
 C、0
D、
2. 在一次函数y=-2x+1的图象上的点是( )A、
C、0
D、
2. 在一次函数y=-2x+1的图象上的点是( )A、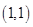 B、
B、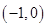 C、
C、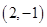 D、
D、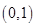 3. 下列各组数分别是直角三角形三边长的是( )A、5,13,13 B、1, , C、1, ,3 D、15,25,354. 下列各式中,正确的是( )A、
3. 下列各组数分别是直角三角形三边长的是( )A、5,13,13 B、1, , C、1, ,3 D、15,25,354. 下列各式中,正确的是( )A、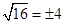 B、
B、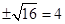 C、
C、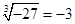 D、
D、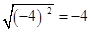 5. 若函数y=(k-1)x|k|+b+1是正比例函数,则k和b的值为( )A、
5. 若函数y=(k-1)x|k|+b+1是正比例函数,则k和b的值为( )A、 ,
, 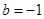 B、
B、 ,
C、 ,
,
C、 , 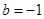 D、 ,
D、 , 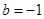 6. 已知直线y=-3x+b经过点A(1,y1)和点B(-2,y2),则y1与y2的大小关系是( )A、
6. 已知直线y=-3x+b经过点A(1,y1)和点B(-2,y2),则y1与y2的大小关系是( )A、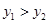 B、
B、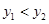 C、
C、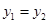 D、不能确定
7. 下列有关一次函数y=-3x+2的说法中,错误的是( )A、当x值增大时,y的值随着x增大而减小 B、 函数图象与y轴的交点坐标为 C、 当 时,
D、不能确定
7. 下列有关一次函数y=-3x+2的说法中,错误的是( )A、当x值增大时,y的值随着x增大而减小 B、 函数图象与y轴的交点坐标为 C、 当 时, D、函数图象经过第一、二、四象限
8. 某人驾车从A地上高速公路前往B地,中途在服务区休息了一段时间.出发时油箱中存油40升,到B地后发现油箱中还剩油4升,则从出发后到B地油箱中所剩油y(升)与时间t(小时)之间函数的大致图象是( )A、
D、函数图象经过第一、二、四象限
8. 某人驾车从A地上高速公路前往B地,中途在服务区休息了一段时间.出发时油箱中存油40升,到B地后发现油箱中还剩油4升,则从出发后到B地油箱中所剩油y(升)与时间t(小时)之间函数的大致图象是( )A、 B、
B、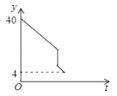 C、
C、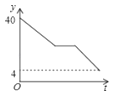 D、
D、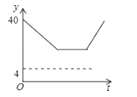 9. 已知函数y=kx+b的图象如图所示,则函数y=-bx+k的图象大致是( )
9. 已知函数y=kx+b的图象如图所示,则函数y=-bx+k的图象大致是( )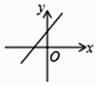 A、
A、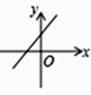 B、
B、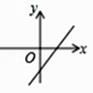 C、
C、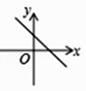 D、
D、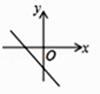 10. 如图所示,一圆柱高8cm,底面半径为2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是( )
10. 如图所示,一圆柱高8cm,底面半径为2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是( )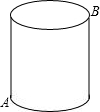 A、20cm B、10cm C、14cm D、无法确定11. 如图,已知l1∥l2∥l3 , 相邻两条平行直线间的距离均为1,若等腰直角△ABC的三个顶点分别在这三条平行直线上,∠C=90°,求AB的长是( )
A、20cm B、10cm C、14cm D、无法确定11. 如图,已知l1∥l2∥l3 , 相邻两条平行直线间的距离均为1,若等腰直角△ABC的三个顶点分别在这三条平行直线上,∠C=90°,求AB的长是( )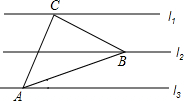 A、3 B、
A、3 B、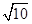 C、
C、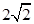 D、
12. 如图,等腰直角三角形纸片ABC中,∠C=90°,把纸片沿EF对折后,点A恰好落在BC上的点D处,点CE=1,AC=4,则下列结论一定正确的个数是( )
D、
12. 如图,等腰直角三角形纸片ABC中,∠C=90°,把纸片沿EF对折后,点A恰好落在BC上的点D处,点CE=1,AC=4,则下列结论一定正确的个数是( )①∠CDE=∠DFB;②BD>CE;③BC= CD;④△DCE与△BDF的周长相等.
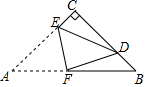 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,则点C到AB的距离CD= .
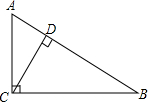 14. 如图,l1表示某个公司一种产品一天的销售收入与销售量的关系,l2表示该公司这种产品一天的销售成本与销售量的关系.当销售量=时,利润为6万元.
14. 如图,l1表示某个公司一种产品一天的销售收入与销售量的关系,l2表示该公司这种产品一天的销售成本与销售量的关系.当销售量=时,利润为6万元.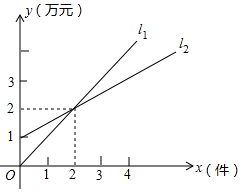 15. 观察下列各式: = -1, = , =2- …请利用你发现的规律计算:
15. 观察下列各式: = -1, = , =2- …请利用你发现的规律计算:( + + +…+ )×( + )= .
三、计算题
-
16. 求满足下列各式的未知数x(1)、x2=(2)、(x-2)3=-12517. 大鹏新区某住宅小区计划购买并种植甲、乙两种树苗共300株.已知甲种树苗每株60元,乙种树苗每株90元.设购买甲种树苗x株,购买两种树苗总费用为y元.(1)、求y与x函数关系式;(2)、若100≤x≤225时,如何购买甲、乙两种树苗才能保证费用最低?最低费用是多少?
四、解答题
-
18. 计算(1)、 -2 +(2)、( + )( - )-19. 如图,在平面直角坐标系中有一个△ABC,顶点A(-1,3),B(2,0),C(-3,-1).
 (1)、画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
(1)、画出△ABC关于y轴的对称图形△A1B1C1(不写画法);点A关于x轴对称的点坐标为
点B关于y轴对称的点坐标为
点C关于原点对称的点坐标为
(2)、若网格上的每个小正方形的边长为1,则△ABC的面积是 .20. 如图,已知直线l1经过点A(0,-1)与点P(2,3),另一条直线l2经过点P,且与y轴交于点B(0,m).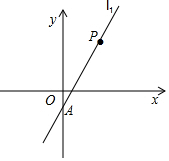 (1)、求直线l1的解析式;(2)、若△APB的面积为3,求m的值.21. 如图1,在等腰Rt△ABC中,∠ACB=90°,点F是AB上一点,作等腰Rt△FCP,且∠PCF=90°,连结AP.
(1)、求直线l1的解析式;(2)、若△APB的面积为3,求m的值.21. 如图1,在等腰Rt△ABC中,∠ACB=90°,点F是AB上一点,作等腰Rt△FCP,且∠PCF=90°,连结AP.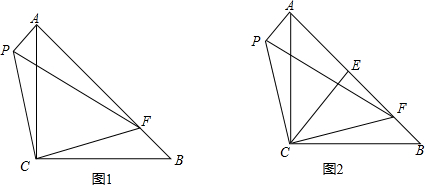 (1)、求证:△CFB≌△CPA;(2)、求证:AP2+AF2=PF2;(3)、如图2,在AF上取点E,使∠ECF=45°,求证:AE2+BF2=EF2 .22. 长方形纸片OABC中,AB=10cm,BC=6cm,把这张长方形纸片OABC如图放置在平面直角坐标系中,在边OA上取一点E,将△ABE沿BE折叠,使点A恰好落在OC边上的点F处.
(1)、求证:△CFB≌△CPA;(2)、求证:AP2+AF2=PF2;(3)、如图2,在AF上取点E,使∠ECF=45°,求证:AE2+BF2=EF2 .22. 长方形纸片OABC中,AB=10cm,BC=6cm,把这张长方形纸片OABC如图放置在平面直角坐标系中,在边OA上取一点E,将△ABE沿BE折叠,使点A恰好落在OC边上的点F处.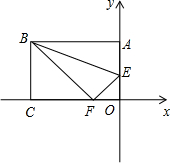 (1)、求点E、F的坐标;(2)、在AB上找一点P,使PE+PF最小,求点P坐标;(3)、在(2)的条件下,点Q(x,y)是直线PF上一个动点,设△OCQ的面积为S,求S与x的函数关系式.
(1)、求点E、F的坐标;(2)、在AB上找一点P,使PE+PF最小,求点P坐标;(3)、在(2)的条件下,点Q(x,y)是直线PF上一个动点,设△OCQ的面积为S,求S与x的函数关系式.