2017年江苏省宿迁市沭阳县中考数学一模试卷
试卷更新日期:2017-04-10 类型:中考模拟
一、选择题
-
1. 在下列实数: 、 、 、 、﹣1.010010001…中,无理数有( )A、1个 B、2个 C、3个 D、4个2. 下列计算中,正确的是( )A、a3+a3=a6 B、(a2)3=a5 C、a2•a4=a8 D、a4÷a3=a3. 不等式组 的正整数解的个数是( )A、1个 B、2个 C、3个 D、4个4. 若关于x的一元二次方程kx2﹣6x+9=0有两个不相等的实数根,则k的取值范围是( )A、k>1 B、k≠0 C、k<1 D、k<1且k≠05. 某部队一位新兵进行射击训练,连续射靶5次,命中的环数分别是0,2,5,2,7.这组数据的中位数与众数分别是( )A、2,5 B、2,2 C、5,7 D、2,76. 若菱形两条对角线的长分别为6和8,则这个菱形的周长为( )A、20 B、16 C、12 D、107. 已知二次函数y=a(x﹣1)2+b(a≠0)有最小值﹣1,则a与b之间的大小关系是( )A、a<b B、a=b C、a>b D、不能确定8.
如图所示,点P(3a,a)是反比例函数y= (k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
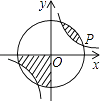 A、y= B、y= C、y= D、y=
A、y= B、y= C、y= D、y=二、填空题
-
9. 数 的相反数是 .10. 银原子的直径为0.0003微米,用科学记数表示为微米.11. 若 = ,则 = .12. 已知 +|2x﹣y|=0,那么x﹣y= .13. 在同一直角坐标平面内,直线y=x与双曲线y= 没有交点,那么m的取值范围是 .14. 四张完全相同的卡片上,分别画有等边三角形、平行四边形、矩形、等腰梯形,现从中随机抽取一张,卡片上画的恰好是中心对称图形的概率为 .15. 等腰三角形的两边长分别是3和5,则这个等腰三角形的周长为 .16. 如图,⊙O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于度.
 17. 在Rt△ABC中,斜边AB=5厘米,BC=a厘米,AC=b厘米,a>b,且a、b是方程x2﹣(m﹣1)x+m+4=0的两根,Rt△ABC的面积为平方厘米.18. 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα= .下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8;④0<CE≤6.4.其中正确的结论是 . (把你认为正确结论的序号都填上)
17. 在Rt△ABC中,斜边AB=5厘米,BC=a厘米,AC=b厘米,a>b,且a、b是方程x2﹣(m﹣1)x+m+4=0的两根,Rt△ABC的面积为平方厘米.18. 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα= .下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8;④0<CE≤6.4.其中正确的结论是 . (把你认为正确结论的序号都填上)
三、解答题
-
19. 计算: +( )﹣1﹣2cos60°+(2﹣π)0 .20. 先化简,后求值: ,其中x=﹣2.21.
如图,在平面直角坐标系中,∠AOB=60°,点B坐标为(2,0),线段OA的长为6.将△AOB绕点O逆时针旋转60°后,点A落在点C处,点B落在点D处.
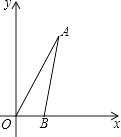 (1)、请在图中画出△COD;(2)、求点A旋转过程中所经过的路程(精确到0.1).22. 如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=25°,求∠APB的度数.
(1)、请在图中画出△COD;(2)、求点A旋转过程中所经过的路程(精确到0.1).22. 如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=25°,求∠APB的度数. 23. 哈市某中学为了解学生的课余生活情况,学校决定围绕“在欣赏音乐、读课外书、体育运动.其他活动中,你最喜欢的课余生活种类是什么?(只写一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查问卷适当整理后绘制成如图所示的不完整的条形统计图,其中最喜欢欣赏音乐的学生占被抽取人数的12%,请你根据以上信息解答下列问题:
23. 哈市某中学为了解学生的课余生活情况,学校决定围绕“在欣赏音乐、读课外书、体育运动.其他活动中,你最喜欢的课余生活种类是什么?(只写一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查问卷适当整理后绘制成如图所示的不完整的条形统计图,其中最喜欢欣赏音乐的学生占被抽取人数的12%,请你根据以上信息解答下列问题: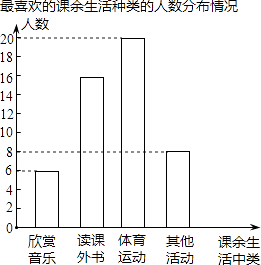 (1)、在这次调查中,一共抽取了多少名学生?(2)、最喜欢读课外书的学生占被抽取人数的百分数是多少?(3)、如果全校有1000名学生,请你估计全校最喜欢体育运动的学生约有多少名?24. 张师傅驾车运送荔枝到某地出售,汽车出发前油箱有油50升,行驶若干小时后,图中在加油站加油若干升,油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
(1)、在这次调查中,一共抽取了多少名学生?(2)、最喜欢读课外书的学生占被抽取人数的百分数是多少?(3)、如果全校有1000名学生,请你估计全校最喜欢体育运动的学生约有多少名?24. 张师傅驾车运送荔枝到某地出售,汽车出发前油箱有油50升,行驶若干小时后,图中在加油站加油若干升,油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示. (1)、汽车行驶小时后加油,中途加油升;(2)、求加油前油箱剩余油量y与行驶时间t的函数关系式;(3)、已知加油前、后汽车都以70千米/小时匀速行驶,如果加油站距目的地210千米,要到达目的地,问油箱中的油是否够用?请说明理由.25. 我市某商场为做好“家电下乡”的惠民服务,决定从厂家购进甲、乙、丙三种不同型号的电视机108台,其中甲种电视机的台数是丙种的4倍,购进三种电视机的总金额不超过147000元,已知甲、乙、丙三种型号的电视机的出厂价格分别为1000元/台,1500元/台,2000元/台.(1)、求该商场至少购买丙种电视机多少台?(2)、若要求甲种电视机的台数不超过乙种电视的台数,问有哪些购买方案?26. 【问题引入】
(1)、汽车行驶小时后加油,中途加油升;(2)、求加油前油箱剩余油量y与行驶时间t的函数关系式;(3)、已知加油前、后汽车都以70千米/小时匀速行驶,如果加油站距目的地210千米,要到达目的地,问油箱中的油是否够用?请说明理由.25. 我市某商场为做好“家电下乡”的惠民服务,决定从厂家购进甲、乙、丙三种不同型号的电视机108台,其中甲种电视机的台数是丙种的4倍,购进三种电视机的总金额不超过147000元,已知甲、乙、丙三种型号的电视机的出厂价格分别为1000元/台,1500元/台,2000元/台.(1)、求该商场至少购买丙种电视机多少台?(2)、若要求甲种电视机的台数不超过乙种电视的台数,问有哪些购买方案?26. 【问题引入】已知:如图BE、CF是△ABC的中线,BE、CF相交于G.求证: = =
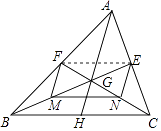
证明:连结EF
∵E、F分别是AC、AB的中点
∴EF∥BC且EF= BC
∴ = = =
【思考解答】
(1)、连结AG并延长AG交BC于H,点H是否为BC中点(填“是”或“不是”)(2)、①如果M、N分别是GB、GC的中点,则四边形EFMN 是四边形.②当 的值为时,四边形EFMN 是矩形.
③当 的值为时,四边形EFMN 是菱形.
④如果AB=AC,且AB=10,BC=16,则四边形EFMN的面积S= .
27.已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连接MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.
 (1)、试直接写出点D的坐标;(2)、已知点B与点D在经过原点的抛物线上,点P在第一象限内的该抛物线上移动,过点P作PQ⊥x轴于点Q,连接OP.
(1)、试直接写出点D的坐标;(2)、已知点B与点D在经过原点的抛物线上,点P在第一象限内的该抛物线上移动,过点P作PQ⊥x轴于点Q,连接OP.①若以O、P、Q为顶点的三角形与△DAO相似,试求出点P的坐标;
②试问在抛物线的对称轴上是否存在一点T,使得|TO﹣TB|的值最大?