2017年江苏省无锡市宜兴市周铁学区联盟中考数学一模试卷
试卷更新日期:2017-04-10 类型:中考模拟
一、选择题
-
1. ﹣2的相反数是( )A、﹣2 B、0 C、2 D、42. 科学家在实验中检测出某微生物约为0.0000035米,将0.0000035用科学记数法表示为( )A、3.5×10﹣6 B、3.5×106 C、3.5×10﹣5 D、35×10﹣53. 下列运算正确的是( )A、(a﹣3)2=a2﹣9 B、a2•a4=a8 C、 =±3 D、 =﹣24. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲
乙
丙
丁
平均数(cm)
185
180
185
180
方差
3.6
3.6
7.4
8.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁5. 下列图形是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( )
6. 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( )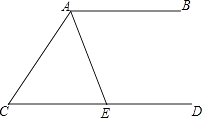 A、65° B、115° C、125° D、130°7. 下列语句正确的是( )A、对角线互相垂直的四边形是菱形 B、有两边及一角对应相等的两个三角形全等 C、矩形的对角线相等 D、平行四边形是轴对称图形8.
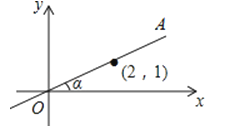
A、65° B、115° C、125° D、130°7. 下列语句正确的是( )A、对角线互相垂直的四边形是菱形 B、有两边及一角对应相等的两个三角形全等 C、矩形的对角线相等 D、平行四边形是轴对称图形8.如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
 A、 B、 C、 D、29. 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
A、 B、 C、 D、29. 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )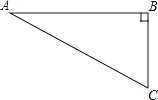 A、 B、 C、 D、10. 如图,在四边形ABCD中,∠ABC=90°,AB=BC=2 ,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
A、 B、 C、 D、10. 如图,在四边形ABCD中,∠ABC=90°,AB=BC=2 ,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( ) A、2 B、 C、 D、3
A、2 B、 C、 D、3二、填空题
-
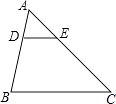
11. 若式子 有意义,则实数x的取值范围是 .12. 分解因式:xy2﹣x= .13. 方程 =1的根是x= .14. 已知圆锥的底面半径是2,母线长是4,则圆锥的侧面积是 .15. 如图,△ABC中,D、E分别在AB、AC上,DE∥BC,AD:AB=1:3,则△ADE与△ABC的面积之比为 .
 16.
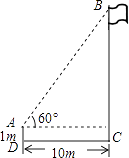
16.如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为 m(结果保留根号).
 17. 如图,点D(0,3),O(0,0),C(4,0),B在⊙A上,BD是⊙A的一条弦.则sin∠OBD= .
17. 如图,点D(0,3),O(0,0),C(4,0),B在⊙A上,BD是⊙A的一条弦.则sin∠OBD= .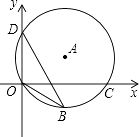 18. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点F在边AC上,并且CF=1,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 .
18. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点F在边AC上,并且CF=1,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 .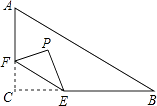
三、解答题
-
19. 计算下列各题:(1)、﹣|﹣1|+ •cos30°﹣(﹣ )﹣2+(π﹣3.14)0 .(2)、(x﹣y)2﹣(x﹣2y)(x+y)20. 解方程与不等式(1)、解方程:x2+3x﹣2=0;(2)、解不等式组: .21. 已知:如图,在菱形ABCD中,点E、F分别为边CD、AD的中点,连接AE,CF,求证:△ADE≌△CDF.
 22. 某学校为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行八百米跑体能测试,测试结果分为A、B、C、D四个等级,请根据两幅统计图中的信息回答下列问题:
22. 某学校为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行八百米跑体能测试,测试结果分为A、B、C、D四个等级,请根据两幅统计图中的信息回答下列问题: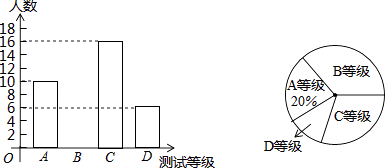 (1)、求本次测试共调查了多少名学生?(2)、求本次测试结果为B等级的学生数,并补全条形统计图;(3)、若该中学八年级共有900名学生,请你估计八年级学生中体能测试结果为D等级的学生有多少人?23. 在一个不透明的袋子中装有白色、黄色和蓝色三种颜色的小球,这些球除颜色外都相同,其中白球有2个,蓝球有1个.现从中任意摸出一个小球是白球的概率是 .(1)、袋子中黄色小球有个;(2)、如果第一次任意摸出一个小球(不放回),第二次再摸出一个小球,请用画树状图或列表格的方法求两次都摸出白球的概率.24. 某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.(1)、按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?(2)、为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.请问至少需要补充多少名新工人?25.
(1)、求本次测试共调查了多少名学生?(2)、求本次测试结果为B等级的学生数,并补全条形统计图;(3)、若该中学八年级共有900名学生,请你估计八年级学生中体能测试结果为D等级的学生有多少人?23. 在一个不透明的袋子中装有白色、黄色和蓝色三种颜色的小球,这些球除颜色外都相同,其中白球有2个,蓝球有1个.现从中任意摸出一个小球是白球的概率是 .(1)、袋子中黄色小球有个;(2)、如果第一次任意摸出一个小球(不放回),第二次再摸出一个小球,请用画树状图或列表格的方法求两次都摸出白球的概率.24. 某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.(1)、按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?(2)、为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.请问至少需要补充多少名新工人?25.如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.
 (1)、求斜坡AB的水平宽度BC;(2)、矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高.(结果保留根号)26. 如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)、求斜坡AB的水平宽度BC;(2)、矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高.(结果保留根号)26. 如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF. (1)、证明:∠E=∠C;(2)、若∠E=55°,求∠BDF的度数;(3)、设DE交AB于点G,若DF=4,cosB= ,E是 的中点,求EG•ED的值.27.
(1)、证明:∠E=∠C;(2)、若∠E=55°,求∠BDF的度数;(3)、设DE交AB于点G,若DF=4,cosB= ,E是 的中点,求EG•ED的值.27.爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.

 (1)、【特例探究】
(1)、【特例探究】如图1,当tan∠PAB=1,c=4 时,a= , b=;
如图2,当∠PAB=30°,c=2时,a= , b=;
(2)、【归纳证明】请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)、【拓展证明】
如图4,▱ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3 ,AB=3,求AF的长.
 28.
28.如图,已知抛物线y=﹣ x2﹣ x+2与x轴交于A、B两点,与y轴交于点C
 (1)、求点A,B,C的坐标;(2)、点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;(3)、此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
(1)、求点A,B,C的坐标;(2)、点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;(3)、此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.