2017年江苏省无锡市宜兴市宜城环科园教学联盟中考数学一模试卷

试卷更新日期：2017-04-10 类型：中考模拟

进入出卷网下载

一、选择题

1. 2的相反数是（）

A、2 B、﹣2 C、﹣ $\frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 函数y= $\sqrt{x - 5}$ 中，自变量x的取值范围是（）

A、x≥﹣5 B、x≤﹣5 C、x≥5 D、x≤5

查看试题解析
3. 某市今年预计建成34个地下调蓄设施，蓄水能力达到140000立方米，将140000用科学记数法表示应为（）

A、14×10⁴ B、1.4×10⁵ C、1.4×10⁶ D、0.14×10⁶

查看试题解析
4. 不等式组 ${\begin{cases} - 2 x < 6 \\ x - 2 > 0 \end{cases}$ 的解集是（）

A、x＞﹣3 B、x＜﹣3 C、x＞2 D、无解

查看试题解析
5. 已知圆锥的底面半径为2cm，母线长为6cm，则圆锥的侧面积是（）

A、24cm² B、24πcm² C、12cm² D、12πcm²

查看试题解析
6. 矩形具有而平行四边形不一定具有的性质是（）

A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、对角相等

查看试题解析
7. 下列图形中，是轴对称图形但不是中心对称图形的是（）

A、等边三角形 B、正六边形 C、正方形 D、圆

查看试题解析
8. 某工厂分发年终奖金，具体金额和人数如下表所示，则下列对这组数据的说法中不正确的是（）
人数
1
3
5
70
10
8
3
金额（元）
200000
150000
80000
15000
10000
8000
5000

A、极差是195000 B、中位数是15000 C、众数是15000 D、平均数是15000

查看试题解析
9. 关于二次函数y=2x²+3，下列说法中正确的是（）

A、它的开口方向是向下 B、当x＜﹣1时，y随x的增大而减小 C、它的顶点坐标是（2，3） D、当x=0时，y有最大值是3

查看试题解析
10. 矩形OABC有两边在坐标轴的正半轴上，如图所示，双曲线y= $\frac{6}{x}$ 与边AB、BC分别交于D、E两点，OE交双曲线y= $\frac{2}{x}$ 于点G，若DG∥OA，OA=3，则CE的长为（）

A、 $\sqrt{2}$ B、1.5 C、 $\sqrt{3}$ D、2

查看试题解析

二、填空题

11. 计算： $\sqrt{\frac{4}{9}}$ = ．

查看试题解析
12. 分解因式：x²﹣25= ．

查看试题解析
13. 方程2x﹣3=0的解是．

查看试题解析
14. 一个正多边形的每个外角都是36°，这个正多边形的边数是．

查看试题解析
15. 如图，AB、BC是⊙O的弦，OM∥BC交AB于M，若∠AOC=100°，则∠AMO=°．

查看试题解析
16.
如图，AB⊥BC，AB=BC=2cm，弧OA与弧OC关于点O中心对称，则AB、BC、弧CO、弧OA所围成的面积是cm² ．

查看试题解析
17. 如图，过D、A、C三点的圆的圆心为E，过B、E、F三点的圆的圆心为D，如果∠A=63°，那么∠B= ．

查看试题解析
18. 如图，矩形ABCD中，点E，F，G，H分别在边AB，BC，CD，DA上，点P在矩形ABCD内．若AB=4cm，BC=6cm，AE=CG=3cm，BF=DH=4cm，四边形AEPH的面积为5cm² ，则四边形PFCG的面积为cm² ．

查看试题解析

三、解答题

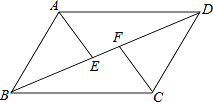
19. 计算下列各题：

(1)、（﹣3）²﹣|﹣2|+（﹣1）⁰+2cos30°

(2)、 $\frac{a^{2} - 2 a + 1}{a - 1}$ ﹣（a﹣2）

查看试题解析
20. 解方程与不等式组

(1)、解方程： $\frac{2}{x} = \frac{3}{x + 3}$ ；

(2)、解不等式组： ${\begin{cases} x - 1 > 2 ， \cdot \cdot \cdot ① \\ x - 3 \leq 2 + \frac{1}{2} ， \cdot \cdot \cdot ② \end{cases}$ ．

查看试题解析
21. 如图，在▱ABCD中，E、F为对角线BD上的两点，且BE=DF．求证：∠BAE=∠DCF．

查看试题解析
22. 一不透明的袋子中装有4个球，它们除了上面分别标有的号码1、2、3、4不同外，其余均相同．将小球搅匀，并从袋中任意取出一球后放回；再将小球搅匀，并从袋中再任意取出一球．若把两次号码之和作为一个两位数的十位上的数字，两次号码之差的绝对值作为这个两位数的个位上的数字，请用“画树状图”或“列表”的方法求所组成的两位数是奇数的概率．

查看试题解析
23. 初三年级教师对试卷讲评课中学生参与的深度与广度进行评价调查，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名初中学生的参与情况，绘制成如图所示的频数分布直方图和扇形统计图（均不完整），请根据图中所给信息解答下列问题：

(1)、在这次评价中，一共抽查了名学生；

(2)、在扇形统计图中，项目“主动质疑”所在的扇形的圆心角的度数为度；

(3)、请将频数分布直方图补充完整；

(4)、如果全市有6000名初三学生，那么在试卷评讲课中，“独立思考”的初三学生约有多少人？

查看试题解析
24. 如图，在△ABC中，AB=AC，∠B=30°，O是BC上一点，以点O为圆心，OB长为半径作圆，恰好经过点A，并与BC交于点D．

(1)、判断直线CA与⊙O的位置关系，并说明理由；

(2)、若AB= $4 \sqrt{3}$ ，求图中阴影部分的面积（结果保留π）．

查看试题解析
25. 在一条直线上依次有A、B、C三个海岛，某海巡船从A岛出发沿直线匀速经B 岛驶向C岛，执行海巡任务，最终达到C岛．设该海巡船行驶x（h）后，与B港的距离为y（km），y与x的函数关系如图所示．

(1)、填空：A、C两港口间的距离为km，a=；

(2)、求y与x的函数关系式，并请解释图中点P的坐标所表示的实际意义；

(3)、在B岛有一不间断发射信号的信号发射台，发射的信号覆盖半径为15km，求该海巡船能接受到该信号的时间有多长？

查看试题解析
26. 做服装生意的王老板经营甲、乙两个店铺，每个店铺在同一段时间内都能售出A、B两种款式的服装合计30件，并且每售出一件A款式和B款式服装，甲店铺获利润分别为30元和35元，乙店铺获利润分别为26元和36元．某日，王老板进A款式服装36件，B款式服装24件，并将这批服装分配给两个店铺各30件．

(1)、怎样将这60件服装分配给两个店铺，能使两个店铺在销售完这批服装后所获利润相同？

(2)、怎样分配这60件服装能保证在甲店铺获利润不小于950元的前提下，王老板获利的总利润最大？最大的总利润是多少？

查看试题解析
27.
如图，在矩形ABCD中，AB=3，BC=4．动点P从点A出发沿AC向终点C运动，同时动点Q从点B出发沿BA向点A运动，到达A点后立刻以原来的速度沿AB返回．点P，Q运动速度均为每秒1个单位长度，当点P到达点C时停止运动，点Q也同时停止．连结PQ，设运动时间为t（t＞0）秒．

(1)、在点Q从B到A的运动过程中，
①当t=时，PQ⊥AC；

(2)、②求△APQ的面积S关于t的函数关系式，并写出t的取值范围；

(3)、伴随着P、Q两点的运动，线段PQ的垂直平分线为l．
①当l经过点A时，射线QP交AD于点E，求AE的长；
②当l经过点B时，求t的值．

查看试题解析
28.
如图1，已知点A（a，0），B（0，b），且a、b满足 $\sqrt{a + 1} + {(a + b + 3)}^{2} = 0$ ，▱ABCD的边AD与y轴交于点E，且E为AD中点，双曲线 $y = \frac{k}{x}$ 经过C、D两点．

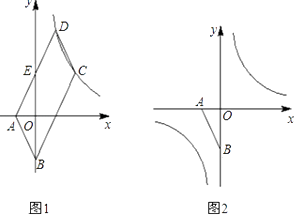(1)、求k的值；

(2)、点P在双曲线 $y = \frac{k}{x}$ 上，点Q在y轴上，若以点A、B、P、Q为顶点的四边形是平行四边形，试求满足要求的所有点P、Q的坐标；

(3)、
以线段AB为对角线作正方形AFBH（如图3），点T是边AF上一动点，M是HT的中点，MN⊥HT，交AB于N，当T在AF上运动时， $\frac{M N}{H T}$ 的值是否发生改变？若改变，求出其变化范围；若不改变，请求出其值，并给出你的证明．

查看试题解析

人数	1	3	5	70	10	8	3
金额（元）	200000	150000	80000	15000	10000	8000	5000