广东省深圳市宝安区2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-01-09 类型:期中考试
一、选择题
-
1. 方程x(x+2)=0的根是( )A、
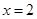 B、
B、 C、
C、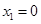 ,
,  D、
D、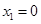 ,
,  2. 下列命题,其中是真命题的为( )A、一组对边平行,另一组对边相等的四边形是平行四边形 B、对角线互相垂直的四边形是菱形 C、对角线相等的四边形是矩形 D、一组邻边相等的矩形是正方形3. 已知m,n是关于x的一元二次方程x2-3x+a=0的两个解,若(m-1)(n-1)=-6,则a的值为( )
2. 下列命题,其中是真命题的为( )A、一组对边平行,另一组对边相等的四边形是平行四边形 B、对角线互相垂直的四边形是菱形 C、对角线相等的四边形是矩形 D、一组邻边相等的矩形是正方形3. 已知m,n是关于x的一元二次方程x2-3x+a=0的两个解,若(m-1)(n-1)=-6,则a的值为( )
A、-10 B、4 C、-4 D、104. 在同一直角坐标系中,函数y= 和y=kx-3的图象大致是( )A、 B、
B、 C、
C、 D、
D、 5. 用配方法解一元二次方程2x2-4x-2=1的过程中,变形正确的是( )A、
5. 用配方法解一元二次方程2x2-4x-2=1的过程中,变形正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 反比例函数y= (k≠0)的图象经过点(-2,3),则该反比例函数图象在( )A、第一,三象限 B、第二,四象限 C、第二,三象限 D、第一,二象限7. 如图,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数y= 在第一象限内的图象经过点D,交BC于点E,若AB=4,CE=2BE, ,则k的值为( )
6. 反比例函数y= (k≠0)的图象经过点(-2,3),则该反比例函数图象在( )A、第一,三象限 B、第二,四象限 C、第二,三象限 D、第一,二象限7. 如图,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数y= 在第一象限内的图象经过点D,交BC于点E,若AB=4,CE=2BE, ,则k的值为( ) A、3 B、 C、6 D、128. 如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD=( )
A、3 B、 C、6 D、128. 如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD=( ) A、 B、
A、 B、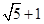 C、4
D、
9. 已知关于x的一元二次方程(m-2)2x2+(2m+1)x+1=0有两个不相等的实数根,则m的取值范围是( )A、
C、4
D、
9. 已知关于x的一元二次方程(m-2)2x2+(2m+1)x+1=0有两个不相等的实数根,则m的取值范围是( )A、 B、
B、 C、
C、 且
且  D、
D、 且
且  10. 如图,在正方形 中, , 分别为 , 的中点, 为对角线 上的一个动点,则下列线段的长等于 最小值的是( )
10. 如图,在正方形 中, , 分别为 , 的中点, 为对角线 上的一个动点,则下列线段的长等于 最小值的是( )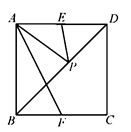 A、 B、 C、 D、11. 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG= ,则△EFC的周长为( )
A、 B、 C、 D、11. 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG= ,则△EFC的周长为( ) A、11 B、10 C、9 D、812. 如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:
A、11 B、10 C、9 D、812. 如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM= MF.其中正确结论的是( )
 A、
A、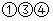 B、
B、 C、
C、
D、
二、填空题
-
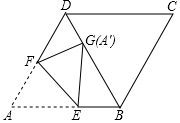
13. 已知: (x、y、z均不为零),则 = .14. 如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为 .
 15. 已知===k,则k的值是 .
15. 已知===k,则k的值是 .
16. 如图,矩形OABC的顶点A,C分别在x轴,y轴上,顶点B在第一象限,AB=1,将线段OA绕点O按逆时针方向旋转60°得到线段OP,连接AP,反比例函数y= (k≠0)的图象经过P,B两点,则k的值为 .
三、解答题
-
17. 解方程:(1)、2(x-3)=3x(x-3)(2)、2x2-x-3=018. 如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
 (1)、请画出△ABC关于x轴对称的△A1B1C1 .(2)、将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得到对应的点A2 , B2 , C2 , 请画出△A2B2C2 .(3)、求△A1B1C1与△A2B2C2的面积比,即 : =(不写解答过程,直接写出结果).19. 如图,利用一面足够长的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏),设矩形ABCD的宽AD为x米,矩形的长为AB(且AB>AD).
(1)、请画出△ABC关于x轴对称的△A1B1C1 .(2)、将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得到对应的点A2 , B2 , C2 , 请画出△A2B2C2 .(3)、求△A1B1C1与△A2B2C2的面积比,即 : =(不写解答过程,直接写出结果).19. 如图,利用一面足够长的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏),设矩形ABCD的宽AD为x米,矩形的长为AB(且AB>AD). (1)、若所用铁栅栏的长为40米,用含x的代数式表示矩形的长AB;(2)、在(1)的条件下,若使矩形场地面积为192平方米,则AD、AB的长应分别为多少米?20. 深圳市民中心广场上有旗杆如图①所示,某学校兴趣小组测量了该旗杆的高度,如图②,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为16米,落在斜坡上的影长CD为8米,AB⊥BC;同一时刻,太阳光线与水平面的夹角为45°。1米的标杆EF竖立在斜坡上的影长FG为2米,求旗杆的高度.
(1)、若所用铁栅栏的长为40米,用含x的代数式表示矩形的长AB;(2)、在(1)的条件下,若使矩形场地面积为192平方米,则AD、AB的长应分别为多少米?20. 深圳市民中心广场上有旗杆如图①所示,某学校兴趣小组测量了该旗杆的高度,如图②,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为16米,落在斜坡上的影长CD为8米,AB⊥BC;同一时刻,太阳光线与水平面的夹角为45°。1米的标杆EF竖立在斜坡上的影长FG为2米,求旗杆的高度. 21. 如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
21. 如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.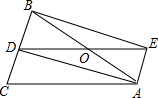 (1)、求证:四边形AEBD是矩形;(2)、当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.22. 如图,在平面直角坐标系中,正比例函数y=kx(k>0)与反比例函数y= 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为(m,0).其中m>0.
(1)、求证:四边形AEBD是矩形;(2)、当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.22. 如图,在平面直角坐标系中,正比例函数y=kx(k>0)与反比例函数y= 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为(m,0).其中m>0. (1)、四边形ABCD的是 . (填写四边形ABCD的形状)(2)、当点A的坐标为(n,3)时,四边形ABCD是矩形,求m,n的值.(3)、试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.23. 在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.
(1)、四边形ABCD的是 . (填写四边形ABCD的形状)(2)、当点A的坐标为(n,3)时,四边形ABCD是矩形,求m,n的值.(3)、试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.23. 在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒. (1)、如图1,当t=3时,求DF的长.(2)、如图2,当点E在线段AB上移动的过程中, 的大小是否发生变化?如果变化,请说明理由;如果不变,请求出 的值.(3)、连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
(1)、如图1,当t=3时,求DF的长.(2)、如图2,当点E在线段AB上移动的过程中, 的大小是否发生变化?如果变化,请说明理由;如果不变,请求出 的值.(3)、连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.