2017年江苏省无锡市宜兴市丁蜀学区中考数学一模试卷
试卷更新日期:2017-04-10 类型:中考模拟
一、选择题
-
1. 4的倒数是( )A、4 B、﹣4 C、 D、﹣2. 下列各式运算中,正确的是( )A、(a+b)2=a2+b2 B、 C、a3•a4=a12 D、3. 式子 在实数范围内有意义,则x的取值范围是( )A、x≥1 B、x≤1 C、x>0 D、x>14. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图,已知圆锥侧面展开图的扇形面积为65πcm2 , 扇形的弧长为10πcm,则圆锥母线长是( )
5. 如图,已知圆锥侧面展开图的扇形面积为65πcm2 , 扇形的弧长为10πcm,则圆锥母线长是( ) A、5cm B、10cm C、12cm D、13cm6. 顺次连接对角线相等的四边形的各边中点,所得图形一定是( )A、平行四边形 B、矩形 C . 菱形 D.正方形7. 下列说法中,你认为正确的是( )A、四边形具有稳定性 B、等边三角形是中心对称图形 C、等腰梯形的对角线一定互相垂直 D、任意多边形的外角和是360°8. ,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这9名同学成绩的( )A、众数 B、中位数 C、平均数 D、极差9. 数学活动课上,四位同学围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”分别作出了下列四个图形.其中作法错误的是( )
A、5cm B、10cm C、12cm D、13cm6. 顺次连接对角线相等的四边形的各边中点,所得图形一定是( )A、平行四边形 B、矩形 C . 菱形 D.正方形7. 下列说法中,你认为正确的是( )A、四边形具有稳定性 B、等边三角形是中心对称图形 C、等腰梯形的对角线一定互相垂直 D、任意多边形的外角和是360°8. ,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这9名同学成绩的( )A、众数 B、中位数 C、平均数 D、极差9. 数学活动课上,四位同学围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”分别作出了下列四个图形.其中作法错误的是( )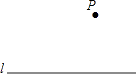 A、
A、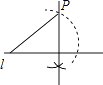 B、
B、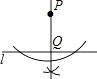 C、
C、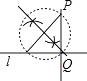 D、
D、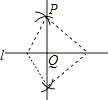 10. 如图,A、B、C是反比例函数y= (x<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )
10. 如图,A、B、C是反比例函数y= (x<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )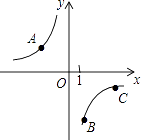 A、4条 B、3条 C、2条 D、1条
A、4条 B、3条 C、2条 D、1条二、填空题
-
11. 3月无锡市商品房平均每平方价格为7500元,7500元用科学记数法表示为元.12. 命题“对顶角相等”的逆命题是命题(填“真”或“假”).13. 分解因式:a3﹣4a= .14. 一元二次方程x2+x﹣2=0的两根之积是 .15. 如图,点O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=38°,则∠OAC的度数是度.
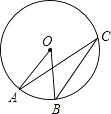 16. 如图,在△ABC和△BAD中,BC=AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是(只填一个).
16. 如图,在△ABC和△BAD中,BC=AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是(只填一个).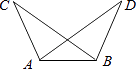 17. 如图,在平面直角坐标系中,点A(a,b)为第一象限内一点,且a<b.连结OA,并以点A为旋转中心把OA逆时针转90°后得线段BA.若点A、B恰好都在同一反比例函数的图象上,则 的值等于
17. 如图,在平面直角坐标系中,点A(a,b)为第一象限内一点,且a<b.连结OA,并以点A为旋转中心把OA逆时针转90°后得线段BA.若点A、B恰好都在同一反比例函数的图象上,则 的值等于 18. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 .
18. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 .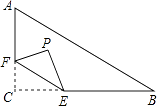
三、解答题
-
19. 计算:
(1)、|﹣2|﹣(1+ )0+ ;(2)、(a﹣ )÷ .20. 解方程与方程组(1)、解方程: + =4.(2)、解不等式组: .21. 如图,平行四边形ABCD的对角线AC、BD,相交于点O,EF过点O且与AB、CD分别相交于点E、F,求证:AE=CF.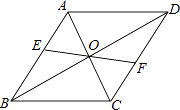 22. 小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).(1)、如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .(2)、如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.(3)、从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)23. 学校为了解学生参加体育活动的情况,对学生“平均每天参加体育活动的时间”进行了随机抽样调查,下图是根据调查结果绘制的两幅不完整的统计图.
22. 小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).(1)、如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .(2)、如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.(3)、从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)23. 学校为了解学生参加体育活动的情况,对学生“平均每天参加体育活动的时间”进行了随机抽样调查,下图是根据调查结果绘制的两幅不完整的统计图.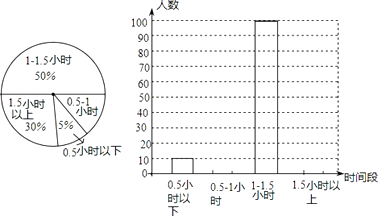
请你根据统计图提供的信息,解答以下问题:
(1)、“平均每天参加体育活动的时间”“为0.5~1小时”部分的扇形统计图的圆心角为度;(2)、本次一共调查了名学生;(3)、将条形统计图补充完整;(4)、若该校有2000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.24. 小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离.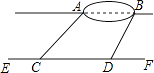 25. 随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.(1)、求一台A型空气净化器和一台B型空气净化器的进价各为多少元?(2)、在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?26.
25. 随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.(1)、求一台A型空气净化器和一台B型空气净化器的进价各为多少元?(2)、在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?26.如图,在平面直角坐标系中,Rt△ABC的顶点A,C分别在y轴,x轴上,∠ACB=90°,OA= ,抛物线y=ax2﹣ax﹣a经过点B(2, ),与y轴交于点D.
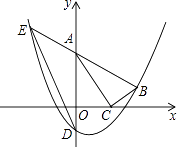 (1)、求抛物线的表达式;(2)、点B关于直线AC的对称点是否在抛物线上?请说明理由;(3)、延长BA交抛物线于点E,连接ED,试说明ED∥AC的理由.27. 在平面直角坐标系xOy中,点P的坐标为(x1 , y1),点Q的坐标为(x2 , y2),且x1≠x2 , y1≠y2 , 若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,如图为点P,Q的“相关矩形”示意图.
(1)、求抛物线的表达式;(2)、点B关于直线AC的对称点是否在抛物线上?请说明理由;(3)、延长BA交抛物线于点E,连接ED,试说明ED∥AC的理由.27. 在平面直角坐标系xOy中,点P的坐标为(x1 , y1),点Q的坐标为(x2 , y2),且x1≠x2 , y1≠y2 , 若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,如图为点P,Q的“相关矩形”示意图.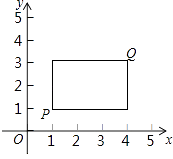 (1)、已知点A的坐标为(1,0),
(1)、已知点A的坐标为(1,0),①若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)、⊙O的半径为 ,点M的坐标为(m,3),若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.28. 问题背景:如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC,BC,CD之间的数量关系.
小吴同学探究此问题的思路是:将△BCD绕点D,逆时针旋转90°到△AED处,点B,C分别落在点A,E处(如图②),易证点C,A,E在同一条直线上,并且△CDE是等腰直角三角形,所以CE= CD,从而得出结论:AC+BC= CD.
简单应用:
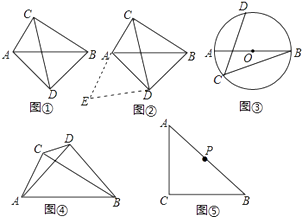 (1)、在图①中,若AC= ,BC=2 ,则CD= .(2)、如图③,AB是⊙O的直径,点C、D在⊙上, = ,若AB=13,BC=12,求CD的长.
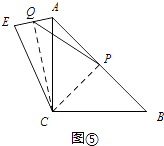
(1)、在图①中,若AC= ,BC=2 ,则CD= .(2)、如图③,AB是⊙O的直径,点C、D在⊙上, = ,若AB=13,BC=12,求CD的长.拓展规律:
(3)、如图④,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m<n),求CD的长(用含m,n的代数式表示)(4)、如图⑤,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE= AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是 .