2017年江苏省无锡市江阴市周庄学区中考数学一模试卷

试卷更新日期：2017-04-10 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣2的倒数是（）

A、2 B、 $\frac{1}{2}$ C、﹣ $\frac{1}{2}$ D、不存在

查看试题解析
2. 下列运算正确的是（）

A、a⁶÷a²=a³ B、a⁵﹣a²=a³ C、（3a³）²=6a⁹ D、2（a³b）²﹣3（a³b）²=﹣a⁶b²

查看试题解析
3. 粤海铁路是我国第一条横跨海峡的铁路通道，设计年输送货物能力为11 000 000吨，用科学记数法应记为（）

A、11×10⁶吨 B、1.1×10⁷吨 C、11×10⁷吨 D、1.1×10⁸吨

查看试题解析
4. 若0＜a＜1，则点M（a﹣1，a）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 若关于x的方程2x﹣m=x﹣2的解为x=3，则m的值为（）

A、﹣5 B、5 C、﹣7 D、7

查看试题解析
6. 如图是由四个相同的小正方体组成的立体图形，它的俯视图为（）

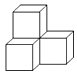A、 B、 C、 D、

查看试题解析
7. 下列调查中，不适合采用抽样调查的是（）

A、了解滨湖区中小学生的睡眠时间 B、了解无锡市初中生的兴趣爱好 C、了解江苏省中学教师的健康状况 D、了解“天宫二号”飞行器各零部件的质量

查看试题解析
8. 如图，⊙A经过点E、B、C、O，且C（0，8），E（﹣6，0），O（0，0），则cos∠OBC的值为（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{3}{16}$

查看试题解析
9. 定义一个新的运算：a⊕b= ${\begin{matrix} - 2 a + b (a \leq b) \\ \frac{b + 2}{- a} (a > b) \end{matrix}$ ，则运算x⊕2的最小值为（）

A、﹣3 B、﹣2 C、2 D、3

查看试题解析
10.
如图1，正方形纸片ABCD的边长为2，翻折∠B、∠D，使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕（如图2）．设AE=x（0＜x＜2），给出下列判断：
①当x=1时，点P是正方形ABCD的中心；
②当x= $\frac{1}{2}$ 时，EF+GH＞AC；
③当0＜x＜2时，六边形AEFCHG面积的最大值是3；
④当0＜x＜2时，六边形AEFCHG周长的值不变．
其中正确的选项是（）

A、①③ B、①②④ C、①③④ D、①②③④

查看试题解析

二、填空题

11. 若 $\frac{1}{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
12. 分解因式：a²﹣2a+1= ．

查看试题解析
13. 在一次信息技术考试中，某兴趣小组8名同学的成绩（单位：分）分别是：7，10，9，8，7，9，9，8，则这组数据的中位数是．

查看试题解析
14. 已知三角形两边长是方程x²﹣5x+6=0的两个根，则三角形的第三边c的取值范围是．

查看试题解析
15. 如图是一个废弃的扇形统计图，小华利用它的阴影部分来制作一个圆锥，则这个圆锥的底面半径是．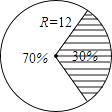

查看试题解析
16. 如图，已知正五边形ABCDE，AF∥CD，交DB的延长线于点F，则∠DFA=度．

查看试题解析
17. 如图，△ABC中，AD⊥BC，垂足为D，AD=BD=3，CD=2，点E从点B出发沿线段BA的方向移动到点A停止，连接CE．若△ADE与△CDE的面积相等，则线段DE的长度是．

查看试题解析
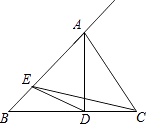18. 如图，矩形OABC的边OA、OC分别在x轴、y轴上，点B的坐标为（7，3），点E在边AB上，且AE=1，已知点P为y轴上一动点，连接EP，过点O作直线EP的垂线段，垂足为点H，在点P从点F（0， $\frac{25}{4}$ ）运动到原点O的过程中，点H的运动路径长为．

查看试题解析

三、解答题

19. 计算下列各题：

(1)、 $\sqrt{4}$ +（ $\frac{1}{2}$ ）^﹣¹﹣2cos60°；

(2)、（2x﹣y）²﹣（x+y）（x﹣y）．

查看试题解析
20. 解方程与方程组

(1)、解方程：x²﹣6x﹣6=0；

(2)、解不等式组： ${\begin{matrix} 3 x - 1 \leq 2 \\ 2 - \frac{x + 4}{2} < \frac{1 - x}{3} \end{matrix}$ ．

查看试题解析
21. 如图，在▱ABCD中，E是AD边上的中点，连接BE，并延长BE交CD的延长线于点F．

(1)、证明：FD=AB；

(2)、当▱ABCD的面积为8时，求△FED的面积．

查看试题解析
22. 2015年合肥市区中考理科实验操作考试备选试题为物理4题（用W₁、W₂、W₃、W₄表示）、化学4题（用H₁、H₂、H₃、H₄表示）、生物2题（用S₁、S₂表示），共10题．某校为备战实验操作考试，对学生进行模拟训练．由学生在每科测试时抽签选定一个进行实验操作．若学生测试时，第一次抽签选定物理实验题，第二次抽签选定化学实验题，第三次抽签选定生物实验题．已知王强同学抽到的物理实验题为 W₁题，

(1)、请用树形图法或列表法，表示王强同学此次抽签的所有可能情况．

(2)、若王强对化学的H₂、H₃y=0.15x和生物的S₁实验准备得较好，求他能同时抽到化学和生物都是准备较好的实验题的概率是多少？

查看试题解析
23. “知识改变命运，科技繁荣祖国”．某区中小学每年都要举办一届科技比赛．如图为某区某校2015年参加科技比赛（包括电子百拼、航模、机器人、建模四个类别）的参赛人数统计图：

(1)、该校参加机器人、建模比赛的人数分别是人和人；

(2)、该校参加科技比赛的总人数是人，电子百拼所在扇形的圆心角的度数是°，并把条形统计图补充完整.

(3)、从全区中小学参加科技比赛选手中随机抽取85人，其中有34人获奖.2015年某区中小学参加科技比赛人数共有3625人，请你估算2015年参加科技比赛的获奖人数约是多少人？

查看试题解析
24. 如图：一辆汽车在一个十字路口遇到红灯刹车停下，汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°，如果斑马线的宽度是AB=3米，驾驶员与车头的距离是0.8米，这时汽车车头与斑马线的距离x是多少？

查看试题解析
25. 文昌某校准备组织学生及学生家长到三亚进行社会实践，为了便于管理，所有人员必须乘坐在同一列火车上；根据报名人数，若都买一等座单程火车票需17010元，若都买二等座单程火车票且花钱最少，则需11220元；已知学生家长与教师的人数之比为2：1，文昌到三亚的火车票价格（部分）如下表所示：
运行区间
公布票价
学生票
上车站
下车站
一等座
二等座
二等座
文昌
三亚
81（元）
68（元）
51（元）

(1)、参加社会实践的老师、家长与学生各有多少人？

(2)、由于各种原因，二等座火车票单程只能买x张（x小于参加社会实践的人数），其余的须买一等座火车票，在保证每位参与人员都有座位坐的前提下，请你设计最经济的购票方案，并写出购买火车票的总费用（单程）y与x之间的函数关系式．

(3)、请你做一个预算，按第（2）小题中的购票方案，购买一个单程火车票至少要花多少钱？最多要花多少钱？

查看试题解析
26.
如图1，在平面直角坐标系中，直线l与x轴、y轴分别交于点B（4，0）、C（0，3），点A为x轴负半轴上一点，AM⊥BC于点M交y轴于点N，满足4CN=5ON．已知抛物线y=ax2+bx+c经过点A、B、C．

(1)、求抛物线的函数关系式；

(2)、连接AC，点D在线段BC上方的抛物线上，连接DC、DB，若△BCD和△ABC面积满足S_△_BCD= $\frac{3}{5}$ S_△_ABC ，求点D的坐标；

(3)、
如图2，E为OB中点，设F为线段BC上一点（不含端点），连接EF．一动点P从E出发，沿线段EF以每秒1个单位的速度运动到F，再沿着线段FC以每秒 $\frac{5}{3}$ 个单位的速度运动到C后停止．若点P在整个运动过程中用时最少，请直接写出最少时间和此时点F的坐标．

查看试题解析
27. 如图，在Rt△ABC中，∠C=90°，AB=50，AC=30，D、E、F分别是AC、AB、BC的中点．点P从点D出发沿折线DE﹣EF﹣FC﹣CD以每秒7个单位长的速度匀速运动；点Q从点B出发沿BA方向以每秒4个单位长的速度匀速运动，过点Q作射线QK⊥AB，交折线BC﹣CA于点G．点P、Q同时出发，当点P绕行一周回到点D时停止运动，点Q也随之停止．设点P、Q运动的时间是t秒（t＞0）．

(1)、D、F两点间的距离是；

(2)、射线QK能否把四边形CDEF分成面积相等的两部分？若能，求出t的值．若不能，说明理由；

(3)、当点P运动到折线EF﹣FC上，且点P又恰好落在射线QK上时，求t的值．

查看试题解析
28. 给出如下规定：两个图形G₁和G₂ ，点P为G₁上任一点，点Q为G₂上任一点，如果线段PQ的长度存在最小值，就称该最小值为两个图形G₁和G₂之间的距离．在平面直角坐标系xOy中，O为坐标原点．

(1)、点A的坐标为A（1，0），则点B（2，3）和射线OA之间的距离为，点C（﹣2，3）和射线OA之间的距离为；

(2)、
如果直线y=x+1和双曲线y= $\frac{k}{x}$ 之间的距离为 $\frac{3 \sqrt{2}}{2}$ ，那么k=；（可在图1中进行研究）

(3)、
点E的坐标为（1， $\sqrt{3}$ ），将射线OE绕原点O顺时针旋转120°，得到射线OF，在坐标平面内所有和射线OE，OF之间的距离相等的点所组成的图形记为图形M．
①请在图2中画出图形M，并描述图形M的组成部分；（若涉及平面中某个区域时可以用阴影表示）．
②将射线OE，OF组成的图形记为图形W，直线y=﹣2x﹣4与图形M的公共部分记为图形N，请求出图形W和图形N之间的距离．

查看试题解析

运行区间	公布票价	学生票
上车站	下车站	一等座	二等座	二等座
文昌	三亚	81（元）	68（元）	51（元）