2017年广东省深圳市龙岗区中考数学一模试卷
试卷更新日期:2017-04-10 类型:中考模拟
一、选择题
-
1. 若关于x的方程x2+3x+a=0有一个根为﹣1,则a的值为( )A、2 B、﹣1 C、﹣2 D、12.
如图是一个用于防震的L形的包装用泡沫塑料,当俯视它时看到的图形形状是( )
 A、
A、 B、
B、 C、
C、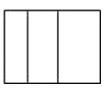 D、
D、 3.
3.如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
 A、6sin75°米 B、米 C、米 D、6tan75°米4. 对于反比例函数y=﹣ ,下列说法不正确的是( )A、图象经过点(1,﹣3) B、图象分布在第二、四象限 C、当x>0时,y随x的增大而增大 D、点A(x1 , y1)、B(x2、y2)都在反比例函数y=﹣ 的图象上,若x1<x2 , 则y1<y25. 周星驰拍摄的电影《美人鱼》取景地在深圳杨梅坑,据称是深圳最美的溪谷,为估计全罗湖区8000名九年级学生去过杨梅坑的人数,随机抽取400名九年级学生,发现其中有50名学生去过该景点,由此估计全区九年级学生中有( )个学生去过该景点.A、1000人 B、800人 C、720人 D、640人6. 将y=x2向上平移2个单位后所得到的抛物线的解析式为( )A、y=x2﹣2 B、y=x2+2 C、y=(x﹣2)2 D、y=(x+2)27. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A、6sin75°米 B、米 C、米 D、6tan75°米4. 对于反比例函数y=﹣ ,下列说法不正确的是( )A、图象经过点(1,﹣3) B、图象分布在第二、四象限 C、当x>0时,y随x的增大而增大 D、点A(x1 , y1)、B(x2、y2)都在反比例函数y=﹣ 的图象上,若x1<x2 , 则y1<y25. 周星驰拍摄的电影《美人鱼》取景地在深圳杨梅坑,据称是深圳最美的溪谷,为估计全罗湖区8000名九年级学生去过杨梅坑的人数,随机抽取400名九年级学生,发现其中有50名学生去过该景点,由此估计全区九年级学生中有( )个学生去过该景点.A、1000人 B、800人 C、720人 D、640人6. 将y=x2向上平移2个单位后所得到的抛物线的解析式为( )A、y=x2﹣2 B、y=x2+2 C、y=(x﹣2)2 D、y=(x+2)27. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( ) A、3:4 B、9:16 C、4:9 D、1:38. 若二次函数的解析式为y=2x2﹣4x+3,则其函数图象与x轴交点的情况是( )A、没有交点 B、有一个交点 C、有两个交点 D、以上都不对9.
A、3:4 B、9:16 C、4:9 D、1:38. 若二次函数的解析式为y=2x2﹣4x+3,则其函数图象与x轴交点的情况是( )A、没有交点 B、有一个交点 C、有两个交点 D、以上都不对9.如图,一农户要建一个矩形花圃,花圃的一边利用长为12m的住房墙,另外三边用25m长的篱笆围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,花圃面积为80m2 , 设与墙垂直的一边长为xm(已标注在图中),则可以列出关于x的方程是( )
 A、x(26﹣2x)=80 B、x(24﹣2x)=80 C、(x﹣1)(26﹣2x)=80 D、x(25﹣2x)=8010. 如图,在平面直角坐标系中,设点P到原点O的距离为ρ,OP与x轴正方向的交角为a,则用[ρ,a]表示点P的极坐标,例如:点P的坐标为(1,1),则其极坐标为[ ,45°].若点Q的极坐标为[4,120°],则点Q的平面坐标为( )
A、x(26﹣2x)=80 B、x(24﹣2x)=80 C、(x﹣1)(26﹣2x)=80 D、x(25﹣2x)=8010. 如图,在平面直角坐标系中,设点P到原点O的距离为ρ,OP与x轴正方向的交角为a,则用[ρ,a]表示点P的极坐标,例如:点P的坐标为(1,1),则其极坐标为[ ,45°].若点Q的极坐标为[4,120°],则点Q的平面坐标为( ) A、(﹣2,﹣2 ) B、(2,﹣2 ) C、(﹣2 ,﹣2) D、(﹣4,﹣4 )11. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个.
A、(﹣2,﹣2 ) B、(2,﹣2 ) C、(﹣2 ,﹣2) D、(﹣4,﹣4 )11. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个. A、1个 B、2个 C、3个 D、4个12. 如图,已知正方形ABCD的边长为4,点E、F分别在边AB、ABC上,且AE=BF=1,CE、DF相交于点O,下列结论:
A、1个 B、2个 C、3个 D、4个12. 如图,已知正方形ABCD的边长为4,点E、F分别在边AB、ABC上,且AE=BF=1,CE、DF相交于点O,下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD= ,④△COD的面积等于四边形BEOF的面积中,正确的有 ( )
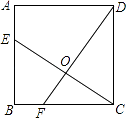 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 已知3x=4y,则 = .14. 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF=cm.
 15. 如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于 .
15. 如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于 . 16. 如图,两个反比例函数y1= (其中k1>0)和y2= 在第一象限内的图象依次是C1和C2 , 点P在C1上,矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为 .
16. 如图,两个反比例函数y1= (其中k1>0)和y2= 在第一象限内的图象依次是C1和C2 , 点P在C1上,矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为 .
三、解答题
-
17. 计算:|﹣ |+(2016﹣π)0﹣2sin45°+( )﹣2 .18. 2017年深圳市男生体育中考考试项目为二项,在200米和1000米两个项目中选一个项目;另外在运球上篮、实心球、跳绳、引体向上四个项目中选一个.(1)、每位男考生一共有种不同的选择方案;(2)、若必胜,必成第一个项目都恰好选了200米,然后在第二组四个项目中各任意选取另外一个用画树状图或列表的方法求必胜和必成选择同种方案的概率.
(友情提醒:各种方案可用A、B、C、…或①、②、③、…等符号来代表可简化解答过程)
19. 如图,一次函数y=ax+b(a≠0)的图形与反比例函数y= (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ,点B的坐标为(m,﹣2). (1)、求该反比例函数和一次函数的解析式.(2)、求△AOC的面积.20.
(1)、求该反比例函数和一次函数的解析式.(2)、求△AOC的面积.20.黄岩岛自古以来就是中国的领土,如图,为维护海洋利益,三沙市一艘海监船在黄岩岛附近海域巡航,某一时刻海监船在A处测得该岛上某一目标C在它的北偏东45°方向,海监船以30海里每小时的速度沿北偏西30°方向航行2小时后到达B处,此时测得该目标C在它的南偏东75°方向.求:
 (1)、∠C的度数;(2)、求该船与岛上目标C之间的距离 即CB的长度(结果保留根号)21. 大梅沙国际风筝节于2016年10月29﹣30日在大梅沙海滨公园举行,老李决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,但每天需支付各种费用共200元,请回答以下问题:(1)、用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);(2)、当售价定为多少时,老李每天获得利润最大,每天的最大利润是多少?22. 如图,点F在▱ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.
(1)、∠C的度数;(2)、求该船与岛上目标C之间的距离 即CB的长度(结果保留根号)21. 大梅沙国际风筝节于2016年10月29﹣30日在大梅沙海滨公园举行,老李决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,但每天需支付各种费用共200元,请回答以下问题:(1)、用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);(2)、当售价定为多少时,老李每天获得利润最大,每天的最大利润是多少?22. 如图,点F在▱ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB. (1)、求证:四边形ABEF是菱形;(2)、若BE=5,AD=8,sin∠CBE= ,求AC的长.23.
(1)、求证:四边形ABEF是菱形;(2)、若BE=5,AD=8,sin∠CBE= ,求AC的长.23.如图,已知抛物线y= x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
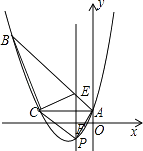 (1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.