2017年安徽省宿州市埇桥区中考数学一模试卷

试卷更新日期：2017-04-10 类型：中考模拟

进入出卷网下载

一、选择题

1. tan60°=（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{2}}{2}$ C、1 D、 $\sqrt{3}$

查看试题解析
2. 如图，在△ABC中，点D、E分别在边AB、AC上，AD：DB=2：3，∠B=∠ADE，则DE：BC等于（）

A、1：2 B、1：3 C、2：3 D、2：5

查看试题解析
3. 若反比例函数y= $\frac{2 a - 3}{x}$ 的图象位于第一、三象限，则a的取值范围是（）

A、a＞0 B、a＞3 C、a＞ $\frac{3}{2}$ D、a＜ $\frac{3}{2}$

查看试题解析
4. 如果关于x的一元二次方程2x²﹣x+k=0有两个实数根，那么k的取值范围是（）

A、k≥ $\frac{1}{8}$ B、k≤ $\frac{1}{8}$ C、k≥﹣ $\frac{1}{8}$ D、k≤﹣ $\frac{1}{8}$

查看试题解析
5. ⊙O过点B，C，圆心O在等腰直角△ABC内部，∠BAC=90°，OA=1，BC=6，则⊙O的半径为（）

A、 $\sqrt{10}$ B、2 $\sqrt{3}$ C、 $\sqrt{13}$ D、3 $\sqrt{2}$

查看试题解析
6. 在如图所示的二次函数y=ax²+bx+c的图象中，大伟同学观察后得出了以下四条结论：①a＜0，b＞0，c＞0；②b²﹣4ac=0；③ $\frac{4 a c - b^{2}}{4 a}$ ＜c；④关于x的一元二次方程ax²+bx+c=0有一个正根，你认为其中正确的结论有（）

A、1条 B、2条 C、3条 D、4条

查看试题解析
7. 铅球的左视图是（）

A、圆 B、长方形 C、正方形 D、三角形

查看试题解析
8. 点P反比例函数y=﹣ $\frac{2 \sqrt{3}}{x}$ 的图象上，过点P分别作坐标轴的垂线段PM、PN，则四边形OMPN的面积=（）

A、 $\sqrt{3}$ B、2 C、2 $\sqrt{3}$ D、1

查看试题解析
9. 从3，1，﹣2这三个数中任取两个不同的数作为M点的坐标，则M点刚好落在第一象限的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
10. 如图，在▱ABCD中，点E、F分别在边AD、BC上，且EF∥CD，G为边AD延长线上一点，连接BG，则图中与△ABG相似的三角形有（）个．

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 如图，E是矩形ABCD的对角线的交点，点F在边AE上，且DF=DC，若∠ADF=25°，则∠BEC= ．

查看试题解析
12. 把抛物线y=﹣2x²+4x﹣5向左平移3个单位后，它与y轴的交点是．

查看试题解析
13. 如图，在正方形ABCD中，点E、F分别在BC、CD上，且BE=DF，若∠EAF=30°，则sin∠EDF= ．

查看试题解析
14. 如图，在Rt△ABC中，∠ACB=90°，∠A=30°，AC=15cm，点O在中线CD上，设OC=xcm，当半径为3cm的⊙O与△ABC的边相切时，x= ．

查看试题解析

三、解答题

15. 在如图的正方形网格中，点O在格点上，⊙O的半径与小正方形的边长相等，请利用无刻度的直尺完成作图，在图（1）中画出一个45°的圆周角，在图（2）中画出一个22.5°的圆周角．

查看试题解析
16. 如图，是用7个相同的正方体积木摆成的几何体的俯视图，请你画出其中一种情况的主视图和它相应的左视图．

查看试题解析
17. 矩形ABCD在坐标系中如图所示放置．已知点B、C在x轴上，点A在第二象限，D（2，4），BC=6，反比例函数y= $\frac{k}{x}$ （x＜0）的图象经过点A．

(1)、求k值；

(2)、把矩形ABCD向左平移，使点C刚好与原点重合，此时线段AB与反比例函数y= $\frac{k}{x}$ 的交点坐标是什么？

查看试题解析
18. 如图，AB是半圆O的直径，点C在圆弧上，D是弧AC的中点，OD与AC相交于点E．求证：△ABC∽△COE．

查看试题解析
19. 设a，b是方程x²+x﹣2016=0的两个不相等的实数根．

(1)、a+b=；ab=；

(2)、求代数式a²+2a+b的值．

查看试题解析
20. 为了了解某水库养殖鱼的有关情况，从该水库多个不同位置捕捞出200条鱼，称得每条鱼的质量（单位：千克），并将所得数据分组，绘制了直方图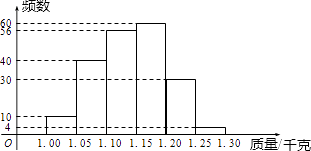

(1)、根据直方图提供的信息，这组数据的中位数落在范围内；

(2)、估计数据落在1.00～1.15中的频率是；

(3)、将上面捕捞的200条鱼分别作一记号后再放回水库．几天后再从水库的多处不同的位置捕捞150条鱼，其中带有记号的鱼有10条，请根据这一情况估算该水库中鱼的总条数．

查看试题解析
21. 如图，某生在旗杆EF与实验楼CD之间的A处，测得∠EAF=60°，然后向左移动12米到B处，测得∠EBF=30°，∠CBD=45°，sin∠CAD= $\frac{3}{5}$ ．

(1)、求旗杆EF的高；

(2)、求旗杆EF与实验楼CD之间的水平距离DF的长．

查看试题解析
22.
如图1所示，将一个边长为2的正方形ABCD和一个长为2、宽为1的矩形CEFD拼在一起，构成一个大的矩形ABEF，现将小矩形CEFD绕点C顺时针旋转，得到矩形CE′F′D′，旋转角为α．

(1)、当点D′恰好落在EF边上时，求旋转角α的值；

(2)、
如图2，G为BC的中点，且0°＜α＜90°，求证：GD′=E′D；

(3)、小矩形CEFD绕点C顺时针旋转一周的过程中，△DCD′与△CBD′能否全等？若能，直接写出旋转角α的值；若不能，说明理由．

查看试题解析
23.
如图，已知抛物线l₁经过原点与A点，其顶点是P（﹣2，3），平行于y轴的直线m与x轴交于点B（b，0），与抛物线l₁交于点M．

(1)、点A的坐标是；抛物线l₁的解析式是；

(2)、当BM=3时，求b的值；

(3)、把抛物线l₁绕点（0，1）旋转180°，得到抛物线l₂ ．
①直接写出当两条抛物线对应的函数值y都随着x的增大而减小时，x的取值范围；

(4)、②直线m与抛物线l₂交于点N，设线段MN的长为n，求n与b的关系式，并求出线段MN的最小值与此时b的值．

查看试题解析