2016-2017学年江苏省常州市金坛市八年级上学期期中数学试卷
试卷更新日期：2017-04-10 类型：期中考试
一、选择题
-
1. 如图，△ABC≌△AEF，则∠EAC等于（ ）
A、∠ACB B、∠CAF C、∠BAF D、∠BAC2. 如图，点B、F、C、E在一条直线上，AB∥DE，AC∥DF，那么添加下列一个条件后，仍无法判断△ABC≌△DEF的是（ ）
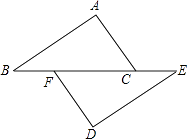A、AB=DE B、∠A=∠D C、AC=DF D、BF=EC3. 如图所示，点D是△ABC的边AC上一点（不含端点），AD=BD，则下列结论正确的是（ ）
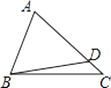A、AC＞BC B、AC=BC C、∠A＞∠ABC D、∠A=∠ABC4. 下列标志中，可以看作是轴对称图形的是（ ）A、
B、
C、
D、
5. 等腰三角形腰长为5，底边长为8，则其底边上的高为（ ）A、3 B、4 C、6 D、106. 如图，在△ABC中，AC的垂直平分线分别交AC、BC于E、D两点，△ABC的周长为23，ABD的周长为15，则EC的长是（ ）
A、3 B、4 C、6 D、87. 如图，∠AOB=90°，OP平分∠AOB，且OP=4，若点C、D分别在OA、OB上，且△PCD为等腰直角三角形，则满足条件的△PCD有（ ）
A、2个 B、3个 C、4个 D、无穷多个8. 有一张直角三角形纸片，两直角边AC=6cm，BC=8cm，将△ABC折叠，使点B与点A重合，折痕为DE（如图），则CD等于（ ）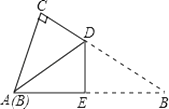
A、 B、 C、 D、二、填空题．
-
9. 直角三角形的斜边长是5，一直角边是3，则此三角形的周长是 ．10. 等腰三角形的周长为10，一边长是2，则等腰三角形的腰长是 ．11. 若△ABC为等腰三角形，顶角∠B=100°，则底角∠A= ．12. 若△ABC三边之比为5：12：13，则△ABC是三角形．13. 如图，点D、E分别在AB、AC上，AD=AE，BD=CE．若∠BDC=80°，则∠AEB= ．
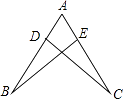14. 如图，在Rt△ABC中，D是斜边AB的中点，若CD=2，则AC2+BC2= ．
15. 如图，在△ABC中，点D是BC上一点，∠BAD=80°，AB=AD=DC，则∠C=度．
16. 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，CD=2，AB=6．设AC=x，BC=y，则代数式（x+y）2﹣3xy+2的值是 ．
三、解答题
-
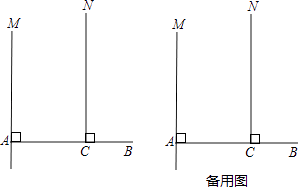
17.
在如图的网格中，
(1)、画△A1B1C1 ， 使它与△ABC关于l1对称；(2)、画△A2B2C2 ， 使它与△A1B1C1关于l2对称；(3)、画出△A2B2C2与ACB的对称轴．
18. 如图，已知∠BAC=∠DCA，∠B=∠D．求证：AB=CD．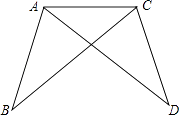
19. 如图，A、B、C、D在同一条直线上，AC=BD，AE=DF，BE=CF．求证：AE∥DF．
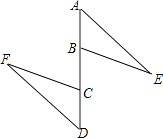20. 如图，已知BC=DE，∠BCF=∠EDF，AF垂直平分CD．求证：∠B=∠E．
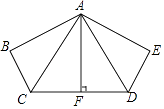21. 如图，△ABC中，AD是高，E、F分别是AB、AC的中点．
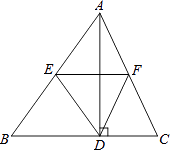(1)、若AB=10，AC=8，求四边形AEDF的周长；(2)、求证：EF垂直平分AD．22. 如图，已知在△ABC中，△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O，MN过点O，且MN∥BC，分别交AB、AC于点M、N．求证：MN=CN﹣BM．
23. 如图，已知四边形ABCD中，AC平分∠BAD，AB=AC=5，AD=3，BC=CD．求点C到AB的距离．
