2016-2017学年吉林省松原市宁江区八年级上学期期中数学试卷

试卷更新日期：2017-04-10 类型：期中考试

进入 出卷网 下载

一、选择题

  • 1. 下面各组线段中，能组成三角形的是（   ）
    A、5，2，3 B、10，5，4 C、4，8，4 D、2，3，4

    查看试题解析

  • 2. 下面四个手机应用图标中是轴对称图形的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 3. 下列尺规作图，能判断AD是△ABC边上的高是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 4. 将一副直角三角板如图放置，使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上，则∠1的度数为（   ）

    A、75° B、65° C、45° D、30°

    查看试题解析

  • 5. 小丽不小心打碎了一块玻璃（如图），玻璃店老板根据涂总阴影部分重新划出一块与原来的玻璃完全相同的玻璃，其根据是（   ）

    A、SAS B、SSS C、ASA D、AAS

    查看试题解析

  • 6. 如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1 ， P2 ， P3 ， P4四个点中找出符合条件的点P，则点P有（   ）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

二、填空题

  • 7. 如图，点A关于x轴的对称点的坐标是 ．

    查看试题解析

  • 8. 等腰三角形的一边长是4cm，另一边长为8cm，其周长为 cm．

    查看试题解析

  • 9. 已知正n边形的每个内角为135度，则这个正多边形的边数n的值为 ．

    查看试题解析

  • 10. 如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是 ．

    查看试题解析

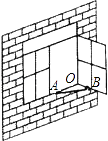  • 11. 如图，△ABC中，AD⊥BC于D，要使△ABD≌△ACD，若根据“HL”判定，还需加条件 ．

    查看试题解析

  • 12. 如图，在等腰三角形ABC中，AB=AC，DE垂直平分AB，已知∠A=50°，则∠DBC=°．

    查看试题解析

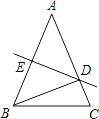  • 13. 如图，OP平分∠AOB，PB⊥OB，OA=8cm，PB=3cm，则△POA的面积等于 cm2 ．

    查看试题解析

  • 14. 如图，直线MN是四边形AMBN的对称轴，点P是直线MN上的点，给出下列判断：

    ①AM=BM；②AP=BN；③∠MAP=∠MBP；④AN∥BP．其中结论正确的是：（填上序号即可）

    查看试题解析

三、解答题

  • 15. 如图，在△ABC中，AB=AC，BD⊥AC于D，若∠ABC=72°，求∠ABD的度数．

    查看试题解析

  • 16. 如图，已知AB∥CD，BC∥DE，若∠A=20°，∠C=120°，求∠AED的度数．

    查看试题解析

  • 17. 如图，有两个长度相等（BC=EF）的滑梯靠在一面墙上，已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，求证：∠ABC+∠DFE=90°．

    查看试题解析

  • 18. 如图，在△ABC和△CED中，AB∥CD，AB=CE，AC=CD．求证：∠B=∠E．

    查看试题解析

四、解答题

  • 19. 雨伞的中截面如图所示，伞骨AB=AC，支撑杆OE=OF，AE= 13 AB，AF= 13 AC，当O沿AD滑动时，雨伞开闭，问雨伞开闭过程中，∠BAD与∠CAD有何关系？说明理由．

    查看试题解析

  • 20.

    如图，在平面直角坐标系中，A（﹣1，5）、B（﹣1，0）、C（﹣4，3）．

    (1)、在图中作出△ABC关于y轴的对称图形△A1B1C1 ．

    (2)、写出点A1、B1、C1的坐标．

    查看试题解析

  • 21. 如图，点B，F，C，E在直线l上（F，C之间不能直接测量），点A，D在l异侧，测得AB=DE，AC=DF，BF=EC．

    (1)、求证：△ABC≌△DEF；
    (2)、指出图中所有平行的线段，并说明理由．

    查看试题解析

  • 22. 如图，已知△ABC中，点D在边AC上，且BC=CD

    (1)、用尺规作出∠ACB的平分线CP（保留作图痕迹，不要求写作法）；
    (2)、在（1）中，设CP与AB相交于点E，连接DE，求证：BE=DE．

    查看试题解析

五、解答题

  • 23. 已知n边形的内角和θ=（n﹣2）×180°．
    (1)、甲同学说，θ能取360°；而乙同学说，θ也能取630°．甲、乙的说法对吗？若对，求出边数n．若不对，说明理由；
    (2)、若n边形变为（n+x）边形，发现内角和增加了360°，用列方程的方法确定x．

    查看试题解析

  • 24. 如图，AD是△ABC的高，BF∥AC，过D点的直线交AC于点E，交BF于点F，DE=DF．

    求证：

    (1)、AB=AC；     
    (2)、BC平分∠ABF．

    查看试题解析

六、解答题

  • 25.

    在等边三角形ABC的边BC上任取一点D，以CD为边向外作等边三角形CDE（如图①），连接AD，BE，易证明BE=AD．

    (1)、若点D在射线BC上（如图②），其他条件均不变，BE=AD是否依然成立？试说明理由；

    (2)、在图②中，若等边三角形CDE与等边三角形ABC均在直线BC的同一侧（如图③），并且B，C，D三点在同一直线上，猜想BE=AD是否依然成立？试说明理由；

    (3)、在（2）的条件下，根据图汇总所标字母，请直接写出你发现的两个正确结论．

    ①；② ．

    查看试题解析

  • 26.

    探究题

    (1)、理解证明：

    如图1，∠MAN=90°，射线AE在这个角的内部，点B，C在∠MAN的边AM，AN上，且AB=AC，CF⊥AE于点F，BD⊥AE于点D．证明△ABD≌△CAF；

    (2)、类比探究：

    如图2，点B，C在∠MAN的边AM、AN上，点E，F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC，∠1=∠2=∠BAC．求证：△ABE≌△CAF；

    (3)、如图3，在△ABC中，AB=AC，AB＞BC．点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为15，则△ACF与△BDE的面积之和为多少？

    查看试题解析