2016-2017学年湖北省孝感市安陆市八年级上学期期中数学试卷
试卷更新日期：2017-04-10 类型：期中考试
一、精心选择，一锤定音
-
1. 在下列各电视台的台标图案中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 到三角形三个顶点的距离都相等的点是这个三角形的（ ）A、三条高的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条边的垂直平分线的交点3.如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（ ）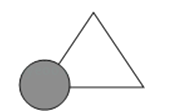
A、SSS B、SAS C、AAS D、ASA4.如图，△ABC中，BO，CO分别是∠ABC，∠ACB的平分线，∠A=50°，则∠BOC等于（ ）
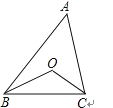A、110° B、115° C、120° D、130°5. 如图所示，点D是△ABC的边AC上一点（不含端点），AD=BD，则下列结论正确的是（ ）
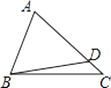A、AC＞BC B、AC=BC C、∠A＞∠ABC D、∠A=∠ABC6. 若等腰三角形一腰上的高和另一腰的夹角为25°，则该三角形的一个底角为（ ）A、32.5° B、57.5° C、65°或57.5° D、32.5°或57.5°7. 如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，则∠A等于（ ）
A、30° B、40° C、36° D、45°8. 如图，四边形ABCD的对角线AC、BD相交于点O，△ABO≌△ADO，下列结论：①AC⊥BD；②CB=CD；③△ABC≌△ADC；④DA=DC．其中所有正确结论的个数有（ ）
A、1个 B、2个 C、3个 D、4个9. 我们都有这样的生活经验，要想使多边形（三角形除外）木架不变形至少再钉上若干根木条，如图所示，四边形至少再钉上一根；五边形至少再钉上两根；六边形至少再钉上三根；…，按照此规律，十二边形至少再钉上（ ）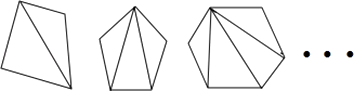
A、11根 B、10根 C、9根 D、8根二、细线填一填，试试自己的身手！
-
10. 在画三角形的三条重要线段（角平分线、中线和高线）时，不一定画在三角形内部的是 ．11. △ABC中，∠B=60°，AB=AC，BC=3，则△ABC的周长为 ．12. 点M（a，﹣5）与点N（﹣2，b）关于x轴对称，则a+b= ．13. 如图所示，△ABC和△A′B′C′是两个全等的三角形，其中某些边的长度及某些角已知，则x= ．
14. 如图，在△ABC中，DE是AC的垂直平分线，AE=3cm，△ABD的周长为13cm，则△ABC的周长是 cm．
15. 如图的七边形ABCDEFG中，AB、ED的延长线相交于O点．若图中∠1、∠2、∠3、∠4的外角的角度和为220°，则∠BOD的度数为 ．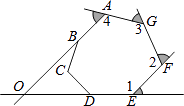
16. 已知：如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，点B，D，E在同一直线上，AF⊥BE于点F，那么线段BE，CE，AF三者之间的数量关系是 ．
17. 如图，已知∠AOB=60°，点P是OA边上，OP=8cm，点M、N在边OB上，PM=PN，若MN=2cm，则ON=cm．
18.如图，线段AB与线段CD关于直线L对称，点P是直线L上一动点，测得：点D与点A之间的距离为8cm，点B与点D之间的距离为5cm，那么PA+PB的最小值是 ．
19. 如图，在△ABC中，∠ABC和∠ACB的平分线相交于点G，过点G作EF∥BC交AB于E，交AC于F，过点G作GD⊥AC于D，下列四个结论：①EF=BE+CF；
②∠BGC=90°+ ∠A；
③点G到△ABC各边的距离相等；
④设GD=m，AE+AF=n，则S△AEF=mn．
其中正确的结论是 ．
三、用心做一做，显显自己的能力！
-
20. 如图，点B、E、C、F在同一条直线上，AB=DE，AC=DF，BE=CF，求证：AB∥DE．
21.如图，方格纸中每个小正方形的边长都是1，△ABC的三个顶点都在格点上．
(1)、画△ABC关于直线MN的对称图形△A1B1C1（不写画法）；(2)、作出△ABC的边BC边上的高AE，垂足为点E．（不写画法）；(3)、△ABC的面积为 ．22. 如图，已知△ABC，∠C=90°，AC＜BC．D为BC上一点，且到A，B两点的距离相等．
(1)、用直尺和圆规，作出点D的位置（不写作法，保留作图痕迹）；(2)、连接AD，若∠B=35°，求∠CAD的度数．23. 若等腰三角形一腰上的中线分周长为6cm或9cm两部分，求这个等腰三角形的底边和腰的长．24. 在等边△ABC外侧作直线AP，点B关于直线AP的对称点为D，连接BD，CD，其中CD交直线AP于点E．(1)、依题意补全图1；
(2)、若∠PAB=30°，求∠ACE的度数；(3)、如图2，若60°＜∠PAB＜120°，判断由线段AB，CE，ED可以构成一个含有多少度角的三角形，并证明．
25. 八年级一班数学兴趣小组在一次活动中进行了探究试验活动，请你和他们一起活动吧．
(1)、【探究与发现】如图1，AD是△ABC的中线，延长AD至点E，使ED=AD，连接BE，写出图中全等的两个三角形
(2)、【理解与应用】填空：如图2，EP是△DEF的中线，若EF=5，DE=3，设EP=x，则x的取值范围是
(3)、已知：如图3，AD是△ABC的中线，∠BAC=∠ACB，点Q在BC的延长线上，QC=BC，求证：AQ=2AD．