2016-2017学年湖北省黄石市阳新县富池片区八年级上学期期中数学试卷

试卷更新日期：2017-04-10 类型：期中考试

进入 出卷网 下载

一、选择题

  • 1. 如图，下列图案是我国几家银行的标志，其中轴对称图形有（   ）

    A、4个 B、3个 C、2个 D、1个

    查看试题解析

  • 2. 一个三角形的三个内角中（   ）
    A、至少有一个钝角 B、至少有一个直角 C、至多有一个锐角 D、至少有两个锐角

    查看试题解析

  • 3. 已知直角三角形中30°角所对的直角边为2cm，则斜边的长为（  ）
    A、2cm B、4cm C、6cm D、8cm

    查看试题解析

  • 4. 下列正多边形中，不能铺满地面的是（　　）

    A、正三角形 B、正四边形 C、正五边形 D、正六边形

    查看试题解析

  • 5. 如图，将两根钢条AA′、BB′的中点 O连在一起，使AA′、BB′能绕着点O自由转动，就做成了一个测量工具，由三角形全等可知A′B′的长等于内槽宽AB，那么判定△OAB≌△OA′B′的理由是（   ）

    A、SAS B、ASA C、SSS D、AAS

    查看试题解析

  • 6. 如图，AC=DF，∠ACB=∠DFE，下列哪个条件不能判定△ABC≌△DEF（   ）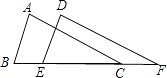

    A、∠A=∠D B、BE=CF C、AB=DE D、AB∥DE

    查看试题解析

  • 7. 已知等腰三角形的周长为10cm，那么当三边为正整数时，它的边长为（   ）
    A、2，2，6 B、3，3，4 C、4，4，2 D、3，3，4或4，4，2

    查看试题解析

  • 8. 如图，△ABC中，∠C=70°，若沿图中虚线截去∠C，则∠1+∠2=（  ）

    A、360° B、250° C、180° D、140°

    查看试题解析

  • 9.

    如图，AD是角平分线，E是AB上一点，AE=AC，EF∥BC交AC于F．下列结论


    ①△ADC≌△ADE；

    ②CE平分∠DEF；

    ③AD垂直平分CE．

    其中正确的个数有（   ）

    A、3 B、2 C、1 D、0

    查看试题解析

  • 10. 如图是一个等边三角形木框，甲虫P在边框AC上爬行（A，C端点除外），设甲虫P到另外两边的距离之和为d，等边三角形ABC的高为h，则d与h的大小关系是（   ）

    A、d＞h B、d＜h C、d=h D、无法确定

    查看试题解析

二、填空题

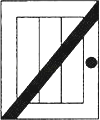
  • 11. 如图，为了使一扇旧木门不变形，木工师傅在木门的背后加钉了一根木条，这样做的道理是 ．

    查看试题解析

  • 12. 在Rt△ABC中，∠A=30°，∠C=90°，AB+BC=12cm，AB= ．

    查看试题解析

  • 13. 一个多边形截去一个角后，形成另一个多边形的内角和为720°，那么原多边形的边数为 ．

    查看试题解析

  • 14. 如图，在△ABC中，AD是高，AE，BF是角平分线，它们相交于点G，AD与BF相交于点H，∠BAC=50°，∠C=70°，则∠AHB= ．

    查看试题解析

  • 15. 如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG=CD，DF=DE，则∠E=度．

    查看试题解析

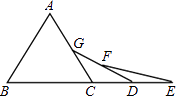  • 16.

    如图，△ABC中，AC=8，AB=10，△ABC的面积为30，AD平分∠BAC，F、E分别为AC、AD上两动点，连接CE、EF，则CE+EF的最小值为 ．

    查看试题解析

三、解答题

  • 17. 已知三角形三边长分别为a、b、c，其中a、b满足（a﹣6）2+|b﹣8|=0，求这个三角形最长边c的取值范围．

    查看试题解析

  • 18.

    如图，在平面直角坐标系中，A（﹣1，5）、B（﹣1，0）、C（﹣4，3）．

    (1)、在图中作出△ABC关于y轴的对称图形△A1B1C1 ．

    (2)、写出点A1、B1、C1的坐标．

    查看试题解析

  • 19. 已知：如图，点C是线段AE的中点，AB=CD，BC=DE．

    求证：△ABC≌△CDE．

    查看试题解析

  • 20. 如图△ABC中，BE是∠ABC的外角平分线，BE交AC的延长线于E，∠A=∠E，求证：∠ACB=3∠A．

    查看试题解析

  • 21. 如图，AD为△ABC的中线，BE为三角形ABD中线．

    (1)、在△BED中作BD边上的高EH；
    (2)、若△ABC的面积为40，BD=5，求EH的长．

    查看试题解析

  • 22. 如图，在四边形ABCD中，∠A=∠C=90°，BE平分∠B，DF平分∠D，求证：BE∥DF．

    查看试题解析

  • 23.

    如图，△ABC是边长为2的等边三角形，D是CA延长线上一点，以BD为边长作等边三角形BDE，连接AE．求：


    ①∠EAD的度数；

    ②求AE﹣AD的值．

    查看试题解析

  • 24.

    如图，已知△ABC中，∠B=∠C，AB=16厘米，BC=12厘米，点D为AB的中点．如果点P在线段BC上以每秒4厘米的速度由B点向C点运动，同时，点Q在线段CA上以每秒a厘米的速度由C点向A点运动，设运动时间为t（秒）（0≤t≤3）．

    (1)、用的代数式表示PC的长度；

    (2)、若点P、Q的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；

    (3)、若点P、Q的运动速度不相等，当点Q的运动速度a为多少时，能够使△BPD与△CQP全等？

    查看试题解析

  • 25. 已知A（0，2），B（4，0）．

    (1)、

    如图1，连接AB，若D（0，﹣6），DE⊥AB于点E，B、C关于y轴对称，M是线段DE上的一点，且DM=AB，连接AM，试判断线段AC与AM之间的位置和数量关系，并证明你的结论；

    (2)、

    如图2，在（1）的条件下，若N是线段DM上的一个动点，P是MA延长线上的一点，且DN=AP，连接PN交y轴于点Q，过点N作NH⊥y轴于点H，当N点在线段DM上运动时，△MQH的面积是否为定值？若是，请求出这个值；若不是，请说明理由．

    查看试题解析