2018-2019学年人教版数学九年级下册 27.2.1 相似三角形的判定 同步练习
试卷更新日期：2019-01-08 类型：同步测试
一、选择题
-
1. 如图，下列四个选项不一定成立的是（ ）
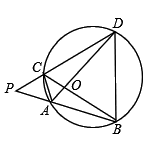A、△COD∽△AOB B、△AOC∽△BOD C、△DCA∽△BAC D、△PCA∽△PBD2. 如图，在△ABC中，点P为AB上一点，给出下列四个条件：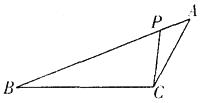
①∠ACP=∠B； ②∠APC=∠ACB；③AC2=AP·AB；④AB·CP=AP·CB．其中能满足△APC和△ACB相似的条件是 （ ）
A、①②④ B、①③④ C、②③④ D、①②③3. 如图所示，在正方形网格上有6个三角形：①△ABC；②△BCD；③△BDE；④△BFG；⑤△FGH；⑥△EFK.其中②～⑥中与①相似的是（ ）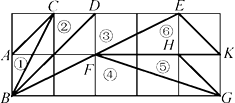
A、②③④ B、③④⑤ C、④⑤⑥ D、②③⑥4. 以下各图放置的小正方形的边长都相同，分别以小正方形的顶点为顶点画三角形，则与△ABC相似的三角形图形为（ ）
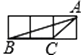A、
B、
C、
D、
5. 下列条件中，不能判断△ABC与△A′B′C′相似的是（ ）A、∠A=45°，∠C=26°，∠A′=45°，∠B′=109° B、AB=1，AC= ，BC=2，A′B′=6，A′C′=9，B′C′=12 C、AB=1.5，AC= ，∠A=36°，A′B′=2.1，A′C′=1.5，∠A′=36° D、AB=2，BC=1，∠C=90°，A′B′= ，B′C′= ，∠B′=90°6. 如图，△ABC中，AB=4，BC=6．点D，点E分别是边AB，BC上的两个动点，若按照下列条件将△ABC沿DE剪开，剪下的△BDE与原三角形不相似的是（ ）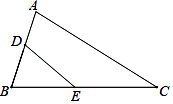
A、∠BDE=∠C B、DE∥AC C、AD=3，BE=2 D、AD=1，CE=47. 下列条件不能判定△ADB∽△ABC的是（ ）
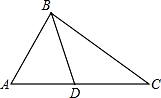A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、 =二、填空题
-
8. 如图所示，点E是平行四边形ABCD的边BC延长线上一点，连接AE，交CD于点F，连接BF．写出图中任意一对相似三角形： ．
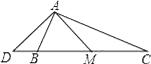
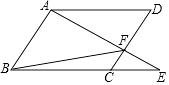9. 如图，在△ABC中，AB≠AC．D、E分别为边AB、AC上的点．AC=3AD，AB=3AE，点F为BC边上一点，添加一个条件： ， 可以使得△FDB与△ADE相似．（只需写出一个）
10. 如图，在边长为1的正方形网格中有点P、A、B、C，则图中所形成的三角形中，相似的三角形是.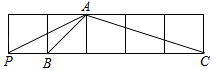
11. 如图，
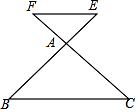(1)、若AE：AB= ， 则△ABC∽△AEF；(2)、若∠E= ， 则△ABC∽△AEF．三、解答题
-
12. 一个三角形的三边长分别为12cm，8cm，7cm，另一个三角形的三边长分别为16cm，24cm，14cm，这两个三角形相似吗？为什么？13. 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，E为BC上一点，连接AE，作EF⊥AE交AB于F．
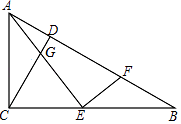(1)、求证：△AGC∽△EFB．(2)、除（1）中相似三角形，图中还有其它相似三角形吗？如果有，请把它们都写出来．14. 如图，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上△ABC和△DEF相似吗？为什么？
15. 已知：如图，在△ABC中，D，E分别为AB、AC边上的点，且AD= AE，连接DE．若AC=3，AB=5．求证：△ADE∽△ACB．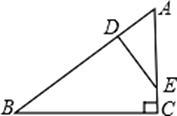
16. 如图，在△ABC中，D、E分别在AB与AC上，且AD=5，DB=7，AE=6，EC=4．求证：△ADE∽△ACB．
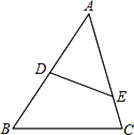17. 如图所示，点D在△ABC的AB边上，AD=2，BD=4，AC=2 ．求证：△ACD∽△ABC．
