2016-2017学年吉林省延边州汪清六中高一上学期期末数学试卷
试卷更新日期：2017-04-10 类型：期末考试
一、选择题
-
1. 设集合U={0，1，2，3，4，5}，M={0，3，5}，N={1，4，5}，则M∩（∁UN）=（ ）A、{5} B、{0，3} C、{0，2，3，5} D、∅2. 已知函数f（x）=x2+1，那么f（a+1）的值为（ ）A、a2+a+2 B、a2+1 C、a2+2a+2 D、a2+2a+13. 如果m＞n＞0，那么下列不等式成立的是（ ）A、log3m＜log3n B、log0.3m＞log0.3n C、3m＜3n D、03m＜0.3n4. 函数f（x）=ex+x﹣2的零点所在的区间是（ ）A、（﹣2，﹣1） B、（﹣1，0） C、（0，1） D、（1，2）5. 下列各图是正方体或正四面体，P，Q，R，S分别是所在棱的中点，这四个点中不共面的一个图是（ ）A、
B、
C、
D、
6. 已知a∥平面α，b⊂α，那么a，b的位置关系是（ ）A、a∥b B、a，b异面 C、a∥b或a，b异面 D、a∥b或a⊥b7. 某四棱锥的三视图如图所示，该四棱锥的表面积是（ ）
A、32 B、16+16 C、48 D、16+328. 长方体的一个顶点上三条棱长分别是3，4，5，且它的8个顶点都在同一球面上，则这个球的表面积是（ ）A、25π B、50π C、125π D、都不对9. 定义在R上的偶函数f（x）满足：对任意的x1 ， x2∈[0，+∞）（x1≠x2），有 ．则（ ）A、f（3）＜f（﹣2）＜f（1） B、f（1）＜f（﹣2）＜f（3） C、f（﹣2）＜f（1）＜f（3） D、f（3）＜f（1）＜f（﹣2）10. 如图，在正方体ABCD﹣A1B1C1D1中，E，F，G，H分别为AA1 ， AB，BB1 ， B1C1的中点，则异面直线EF与GH所成的角等于（ ）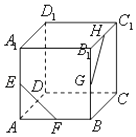
A、45° B、60° C、90° D、120°二、填空题
-
11. 若函数f（x）=（a﹣2）x2+（a﹣1）x+3是偶函数，则a= ．12. 函数f（x）= 的定义域是 ．13. 若2a=5b=10，则 = ．14. 如图，△ABC是直角三角形，∠ACB=90°，PA⊥平面ABC，此图形中有个直角三角形．
15. 将正方形ABCD沿对角线BD折成直二面角A﹣BD﹣C，有如下四个结论：（1）AC⊥BD；
（2）△ACD是等边三角形
（3）AB与平面BCD所成的角为60°；
（4）AB与CD所成的角为60°．
则正确结论的序号为 ．
三、解答题
-
16. 综合题。(1)、计算：2 × ×(2)、计算：2log510+log50.25．17. 已知E、F、G、H为空间四边形ABCD的边AB、BC、CD、DA上的点，且EH∥FG．求证：EH∥BD．
