2018-2019学年人教版数学九年级下册 26.2 实际问题与反比例函数 同步练习
试卷更新日期:2019-01-08 类型:同步测试
一、选择题
-
1. 已知水池的容量为50米3 , 每时灌水量为n米3 , 灌满水所需时间为t(时),那么t与n之间的函数关系式是( )A、t=50n B、t=50﹣n C、t= D、t=50+n2. 小明乘车从南充到成都,行车的速度 和行车时间 之间的函数图象是( )
A、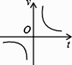 B、
B、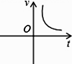 C、
C、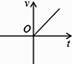 D、
D、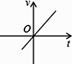 3. 某乡粮食总产量为a(常数)吨,设该乡平均每人占有粮食为y吨,人口数为x,则y与x之间的函数关系的图象是( )
3. 某乡粮食总产量为a(常数)吨,设该乡平均每人占有粮食为y吨,人口数为x,则y与x之间的函数关系的图象是( )
A、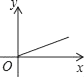 B、
B、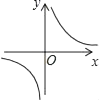 C、
C、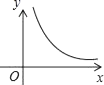 D、
D、 4. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压 p(kPa)是气体体积 V(m 3)的反比例函数,其图象如图所示.当气球内的气压大于140kPa时,气球将爆炸,为了安全起见,气体体积应( )
4. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压 p(kPa)是气体体积 V(m 3)的反比例函数,其图象如图所示.当气球内的气压大于140kPa时,气球将爆炸,为了安全起见,气体体积应( )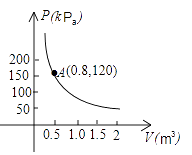 A、不大于 m3 B、不小于 m3 C、不大于 m 3 D、不小于 m 3
A、不大于 m3 B、不小于 m3 C、不大于 m 3 D、不小于 m 3二、填空题
-
5. 某高速公路全长为 ,那么汽车行完全程所需的时间 与行驶的平均速度 之间的关系式为 .6. 某户家庭用购电卡购买了2 000度电,若此户家庭平均每天的用电量为x(单位:度),这2 000度电能够使用的天数为y(单位:天),则y与x的函数关系式为y=.
7. 某厂有煤1500吨,求得这些煤能用的天数y与每天用煤的吨数x之间的函数关系为 .
8. 近视眼镜的度数y度与镜片焦距x米呈反比例,其函数关系式为 如果近似眼镜镜片的焦距 米,那么近视眼镜的度数y为 .
9. 某中学要在校园内划出一块面积为100m2的三角形土地做花圃,设这个三角形的一边长为xm,这条边上的高为ym,那么y关于x的函数解析式是 , 它是一个函数.
10. 某种蓄电池的电压为定值,使用此电源时,电流 与可变电阻 之间的函数关系如图所示,当用电器的电流为 时,用电器的可变电阻为 .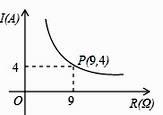 11. 某医药研究所开发一种新药,成年人按规定的剂量限用,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的函数关系近似满足如图所示曲线,当每毫升血液中的含药量不少于0.25毫克时治疗有效,则服药一次治疗疾病有效的时间为.
11. 某医药研究所开发一种新药,成年人按规定的剂量限用,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的函数关系近似满足如图所示曲线,当每毫升血液中的含药量不少于0.25毫克时治疗有效,则服药一次治疗疾病有效的时间为.
三、解答题
-
12. 已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货,设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时)。(1)、求v关于t的函数表达式(2)、若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?13. 厚坝镇某生态示范村种植基地计划用90亩~120亩的土地种植一批葡萄,原计划总产量要达到36万斤.
(1)、列出原计划种植亩数y(亩)与平均每亩产量x(万斤)之间的函数关系式,并写出自变量x的取值范围;
(2)、为了满足市场需求,现决定改良葡萄品种.改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万斤,种值亩数减少了20亩,原计划和改良后的平均每亩产量各是多少万斤?14. 某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走:(1)、假如每天能运x立方米,所需时间为y天,写出y与x之间的函数表达式;
(2)、若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)、在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?15. 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为 的条件下生长最快的新品种.下图是某天恒温系统从开启到关闭及关闭后,大棚内温度 随时间 (小时)变化的函数图象,其中 段是双曲线 的一部分.请根据图中信息解答下列问题: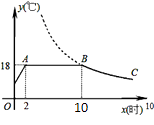 (1)、恒温系统在这天保持大棚内温度 的时间有小时;
(1)、恒温系统在这天保持大棚内温度 的时间有小时;
(2)、当 时,大棚内的温度约为多少度?16. 为了预防流感,某学校在休息天用药薰消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题: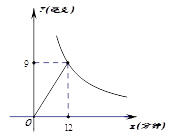 (1)、写出从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(1)、写出从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)、据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
17. 病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量y(毫克)与时间x(小时)满足:前1小时内成正比例递增,1小时后按反比例函数图象衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.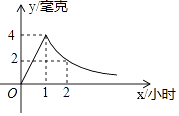 (1)、求函数y(毫克)与x(小时)之间的函数解析式;(2)、已知每毫升血液中含药量不低于0.5毫克时有治疗效果,低于0.5毫克时无治疗效果.求病人一次服药后的有效治疗时间为多少小时?18. 心理学研究发现,一般情况下,在一节 分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数 随时间 (分钟)的变化规律如下图所示(其中 、 分别为线段, 为双曲线的一部分).
(1)、求函数y(毫克)与x(小时)之间的函数解析式;(2)、已知每毫升血液中含药量不低于0.5毫克时有治疗效果,低于0.5毫克时无治疗效果.求病人一次服药后的有效治疗时间为多少小时?18. 心理学研究发现,一般情况下,在一节 分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数 随时间 (分钟)的变化规律如下图所示(其中 、 分别为线段, 为双曲线的一部分).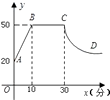 (1)、求注意力指标数 与时间 (分钟)之间的函数关系式;
(1)、求注意力指标数 与时间 (分钟)之间的函数关系式;
(2)、开始学习后第 分钟时与第 分钟时相比较,何时学生的注意力更集中?
(3)、某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知;自主探索,合作交流;总结归纳,巩固提高”.其中“教师引导,回顾旧知”环节 分钟;重点环节“自主探索,合作交流”这一过程一般需要 分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于 .请问这样的课堂学习安排是否合理?并说明理由.19. 码头工人每天往一艘轮船上装载货物,装载速度y(吨/天)与装完货物所需时间x(天)之间的函数关系如图. (1)、求y与x之间的函数表达式;
(1)、求y与x之间的函数表达式;
(2)、由于遇到紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸多少吨货物?
(3)、若原有码头工人10名,装载完毕恰好用了8天时间,在(2)的条件下,至少需要增加多少名工人才能完成任务?