广东省河源市东源县2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-01-08 类型:期中考试
一、选择题
-
1. 下列方程是一元二次方程的是( )A、ax2+bx+c=0 B、
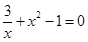 C、2x2-x+2=0
D、4x-1=0
2. 下列图形中,是中心对称图形,但不是轴对称图形的是( )A、正方形 B、矩形 C、菱形 D、平行四边形3. 一元二次方程x2-2x-3=0配方后可变形为( )A、(x-1)2=2 B、(x-1)2=4 C、(x-1)2=1 D、(x-1)2=74. △ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为( )A、1:4 B、1:3 C、1:2 D、1:165. 已知一个不透明的盒子中装有3个红球,2个白球,这些球除颜色外均相同,现从盒中任意摸出一球,则摸到红球的概率是( )A、 B、 C、
C、2x2-x+2=0
D、4x-1=0
2. 下列图形中,是中心对称图形,但不是轴对称图形的是( )A、正方形 B、矩形 C、菱形 D、平行四边形3. 一元二次方程x2-2x-3=0配方后可变形为( )A、(x-1)2=2 B、(x-1)2=4 C、(x-1)2=1 D、(x-1)2=74. △ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为( )A、1:4 B、1:3 C、1:2 D、1:165. 已知一个不透明的盒子中装有3个红球,2个白球,这些球除颜色外均相同,现从盒中任意摸出一球,则摸到红球的概率是( )A、 B、 C、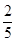 D、
6. 如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是( )
D、
6. 如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是( )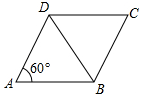 A、1 B、 C、2 D、7. 关于x的一元二次方程x2-3x+m=0有两个不相等的实数根,则实数m的取值范围是( )A、
A、1 B、 C、2 D、7. 关于x的一元二次方程x2-3x+m=0有两个不相等的实数根,则实数m的取值范围是( )A、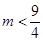 B、
B、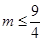 C、
C、 D、
D、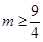 8. 如图,在长100m,宽80m的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644m2 . 设道路的宽为xm,则x满足的方程是( )
8. 如图,在长100m,宽80m的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644m2 . 设道路的宽为xm,则x满足的方程是( )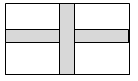 A、100×80-100x-80x=7644 B、(100-x)(80-x)=7644 C、100x+80x=1008×80-7644 D、(100-x)(80-x)+x2=76449. 如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( )
A、100×80-100x-80x=7644 B、(100-x)(80-x)=7644 C、100x+80x=1008×80-7644 D、(100-x)(80-x)+x2=76449. 如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( ) A、
A、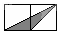 B、
B、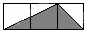 C、
C、 D、
D、 10. 如图所示,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点0,下列结论①AE=BF;②AE⊥BF:③A0=0E:④S△A0B=S四边形DE0F中,正确的有( )
10. 如图所示,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点0,下列结论①AE=BF;②AE⊥BF:③A0=0E:④S△A0B=S四边形DE0F中,正确的有( )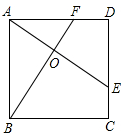 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
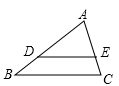
11. 方程x2-9=0的解是 .12. 如果 ,则 =.13. 如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则CE的长为.
 14. 已知菱形的两条对角线长分别为8cm、6cm,则它的边长为cm.15. 在一个不透明的盒子里有2个红球和n个白球,这些球除颜色外其余完全相同.摇匀后随机摸出一个,摸到红球的概率是 ,则n的值为 .16. 如图,折叠矩形纸片ABCD,先折出折痕BD,再折叠使AD边与对角线BD重合,得折痕DG,若AB=8,BC=6,则AG的长是.
14. 已知菱形的两条对角线长分别为8cm、6cm,则它的边长为cm.15. 在一个不透明的盒子里有2个红球和n个白球,这些球除颜色外其余完全相同.摇匀后随机摸出一个,摸到红球的概率是 ,则n的值为 .16. 如图,折叠矩形纸片ABCD,先折出折痕BD,再折叠使AD边与对角线BD重合,得折痕DG,若AB=8,BC=6,则AG的长是.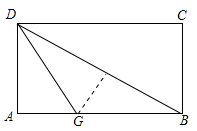
三、解答题(一)
-
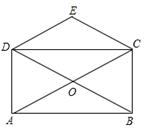
17. 解方程:x(x-2)=3(x-2)18. 已知2是方程x2-3x+c=0的一个根,求方程的另一个根及c的值.19. 如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,求四边形CODE的周长.
四、解答题(二)
-
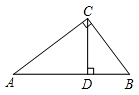
20. 四张小卡片上分别写有数字1、2、3、4.它们除数字外没有任何区别,现将它们放在盒子里搅匀.(1)、随机地从盒子里抽取一张,求抽到数字2的概率;(2)、随机地从盒子里拙取一张.不放回再抽取第二张.请你用画树状图或列表的方法表示所有等可能的结果,并求抽到的数字之和为5的概率.21. 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上高,若AC=12,BC=5,
 (1)、求证:△ABC △CBD;(2)、求CD的长.22. 某市为打造“绿色城市”,积极投入资金进行河道治污与园林绿化两项工程,已知2016年投资1000万元,预计2018年投资1210万元.若这两年内平均每年投资增长的百分率相同.(1)、求平均每年投资增长的百分率;(2)、按此增长率,计算2019年投资额能否达到1360万元?
(1)、求证:△ABC △CBD;(2)、求CD的长.22. 某市为打造“绿色城市”,积极投入资金进行河道治污与园林绿化两项工程,已知2016年投资1000万元,预计2018年投资1210万元.若这两年内平均每年投资增长的百分率相同.(1)、求平均每年投资增长的百分率;(2)、按此增长率,计算2019年投资额能否达到1360万元?五、解答题(三)
-
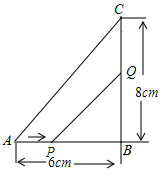
23. 某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”儿童节,商场决定采取适当的降价措施.经调查,如果每件童装降1元,那么平均每天就可多售出2件.(1)、设每件童装应降价x元时,每件盈利元,每天可销售件;(用含x的代数式表示)(2)、每件童装应降价多少元时,平均每天盈利1200元.24. 如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿AB边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动)。如果P、Q分别从A、B两点同时出发,设运动时间为t秒。
 (1)、则:BQ=cm:BP=cm;(用含t的代数式表示)(2)、经过几秒钟,△PBQ的面积等于△ABC的三分之一?(3)、经几秒钟△PBQ与△ABC相似?试说明理由.25. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)、则:BQ=cm:BP=cm;(用含t的代数式表示)(2)、经过几秒钟,△PBQ的面积等于△ABC的三分之一?(3)、经几秒钟△PBQ与△ABC相似?试说明理由.25. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.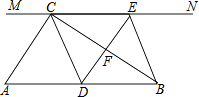 (1)、求证:CE=AD;(2)、当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)、若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
(1)、求证:CE=AD;(2)、当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)、若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.