湖北省部分重点中学2018-2019学年高三上学期理数期中考试试卷
试卷更新日期:2019-01-08 类型:期中考试
一、单选题
-
1. 若复数z满足 ,则z的共轭复数的虚部为A、i B、
 C、
C、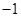 D、1
2. 函数f(x)=xa满足f(2)=4,那么函数g(x)=|loga(x+1)|的图象大致为( )A、
D、1
2. 函数f(x)=xa满足f(2)=4,那么函数g(x)=|loga(x+1)|的图象大致为( )A、 B、
B、 C、
C、 D、
D、 3. 已知集合 , ,则 ( )A、
3. 已知集合 , ,则 ( )A、 B、
B、 C、
C、 D、
D、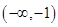 4. 设函数 ,且 ,则k=( )A、0 B、-1 C、3 D、-65. 已知等比数列 的各项都是正数,且 成等差数列,则A、
4. 设函数 ,且 ,则k=( )A、0 B、-1 C、3 D、-65. 已知等比数列 的各项都是正数,且 成等差数列,则A、 B、
B、 C、
D、
C、
D、 6. 已知向量 在向量 方向上的投影为 ,向量 在向量 方向上的投影为 ,且 ,则 ( )A、 B、4 C、2 D、127. 在平面几何中,与三角形的三条边所在直线的距离相等的点有且只有四个.类似的:在立体几何中,与正四面体的六条棱所在直线的距离相等的点( )A、有且只有一个 B、有且只有三个 C、有且只有四个 D、有且只有五个8. 下列四个结论:
6. 已知向量 在向量 方向上的投影为 ,向量 在向量 方向上的投影为 ,且 ,则 ( )A、 B、4 C、2 D、127. 在平面几何中,与三角形的三条边所在直线的距离相等的点有且只有四个.类似的:在立体几何中,与正四面体的六条棱所在直线的距离相等的点( )A、有且只有一个 B、有且只有三个 C、有且只有四个 D、有且只有五个8. 下列四个结论:命题“ , ”的否定是“ , ”; 若 是真命题,则 可能是真命题; “ 且 ”是“ ”的充要条件; ,都有 .其中正确的是
A、 B、
B、 C、
C、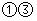 D、
D、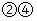 9. 已知 是函数 的最大值,若存在实数 使得对任意实数 总有 成立,则 的最小值为( )A、
9. 已知 是函数 的最大值,若存在实数 使得对任意实数 总有 成立,则 的最小值为( )A、 B、
B、 C、
C、 D、
D、 10. 如图, 的一内角 , , , 边上的中垂线 交 、 分别于 、 两点,则 值为( )
10. 如图, 的一内角 , , , 边上的中垂线 交 、 分别于 、 两点,则 值为( ) A、
A、 B、
C、
B、
C、 D、
D、 11. 已知函数 ,若 满足 ,则 的取值范围是( )A、
11. 已知函数 ,若 满足 ,则 的取值范围是( )A、 B、
B、 C、(-1,1)
D、[-1,1]
12. 若函数 满足 ,且 ,则 的解集为 ( )A、
C、(-1,1)
D、[-1,1]
12. 若函数 满足 ,且 ,则 的解集为 ( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 若 , ,且 ,则由实数a组成的集合14. 已知函数 , 是 的导函数,若 ,则 .15. 已知 ,若 恒成立,则实数 的取值范围是 .16. 已知函数 ,实数 且 ,满足 ,则 的取值范围是 .
三、解答题
-
17. 已知函数(1)、求 的最小正周期和最值(2)、设 ,且 求 的值。18. 已知数列 的前三项与数列 的前三项对应相等,且 对任意的 都成立,数列 是等差数列 求数列 与 的通项公式.19. 已知函数 的部分图像如图所示,其中 、 分别为函数 的一个最高点和最低点, 、 两点的横坐标分别为 ,且 .

(Ⅰ)求函数 的最小正周期和单调递增区间;
(Ⅱ)在 中,角 的对边分别是 ,且满足 ,求 的值.
20. 已知函数 为常数 .(1)、若 是函数 的一个极值点,求此时函数 的单调区间;(2)、若对任意的 , ,不等式 恒成立,求实数m的取值范围.