河南省名校联盟尖子生2018-2019学年高三上学期理数期中考试试卷
试卷更新日期:2019-01-08 类型:期中考试
一、单选题
-
1. 已知集合 , ,则 ( )A、
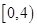 B、
B、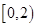 C、
C、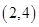 D、
D、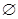 2. 若在复平面内,复数 所对应的点落在直线 上,则A、
2. 若在复平面内,复数 所对应的点落在直线 上,则A、 B、
B、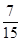 C、
C、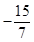 D、
D、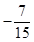 3. 《九章算术》中第七卷“盈不足”问题中有这样一则:“今有蒲生一日,长三尺;莞生一日,长一尺.蒲生日自半,莞生日自倍.”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日加倍.若第n天(n∈R)蒲、莞的长度相等,则第[n]天蒲长了( )尺.(其中[n]表示不超过n的最大整数)A、2 B、 C、1 D、4. 运行如图所示的程序框图,输出的k的值为( )
3. 《九章算术》中第七卷“盈不足”问题中有这样一则:“今有蒲生一日,长三尺;莞生一日,长一尺.蒲生日自半,莞生日自倍.”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日加倍.若第n天(n∈R)蒲、莞的长度相等,则第[n]天蒲长了( )尺.(其中[n]表示不超过n的最大整数)A、2 B、 C、1 D、4. 运行如图所示的程序框图,输出的k的值为( )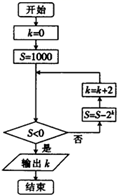 A、8 B、10 C、12 D、145. 已知命题p: ;命题q: , , ,则下列命题中的真命题是A、q B、
A、8 B、10 C、12 D、145. 已知命题p: ;命题q: , , ,则下列命题中的真命题是A、q B、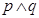 C、
C、 D、
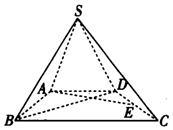
D、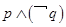 6. 如图所示, 是等腰直角三角形,且 ,E为BC边上的中点, 与 为等边三角形,点M是线段AB与线段DE的交点,点N是线段 与线段EF的交点,若往 中任意投掷一点,该点落在图中阴影区域内的概率为 参考数据: ,
6. 如图所示, 是等腰直角三角形,且 ,E为BC边上的中点, 与 为等边三角形,点M是线段AB与线段DE的交点,点N是线段 与线段EF的交点,若往 中任意投掷一点,该点落在图中阴影区域内的概率为 参考数据: ,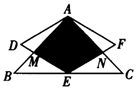 A、
A、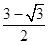 B、
B、 C、
C、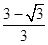 D、
D、 7. 已知某几何体的三视图如下图所示,则在该几何体的所有顶点中任取两点,它们之间的距离不可能为( )
7. 已知某几何体的三视图如下图所示,则在该几何体的所有顶点中任取两点,它们之间的距离不可能为( )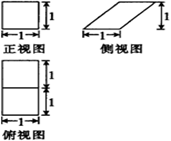 A、
A、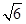 B、
C、2
D、
8. 已知双曲线C: (a>b>0)的两条渐近线与圆O:x2+y2=5交于M,N,P,Q四点,若四边形MNPQ的面积为8,则双曲线C的渐近线方程为( )A、y=± x B、y=± x C、y=±
B、
C、2
D、
8. 已知双曲线C: (a>b>0)的两条渐近线与圆O:x2+y2=5交于M,N,P,Q四点,若四边形MNPQ的面积为8,则双曲线C的渐近线方程为( )A、y=± x B、y=± x C、y=±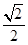 x
D、y=±
x
D、y=± 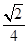 x
9. 已知函数f(x)= +cosx的图象关于y轴对称,若函数g(x)恒满足g(k+x)+g(3-x)+2=0,则函数g(x)的图象的对称中心为( )A、(1,1) B、(2,-1) C、(2,1) D、(1,-1)10. 已知函数 ,若有且仅有两个不同的实数 , ,使得 则实数 的值不可能为A、
x
9. 已知函数f(x)= +cosx的图象关于y轴对称,若函数g(x)恒满足g(k+x)+g(3-x)+2=0,则函数g(x)的图象的对称中心为( )A、(1,1) B、(2,-1) C、(2,1) D、(1,-1)10. 已知函数 ,若有且仅有两个不同的实数 , ,使得 则实数 的值不可能为A、 B、
B、 C、
C、 D、
D、 11. 如图所示,A1 , A2是椭圆C: 的短轴端点,点M在椭圆上运动,且点M不与A1 , A2重合,点N满足NA1⊥MA1 , NA2⊥MA2 , 则 =( )
11. 如图所示,A1 , A2是椭圆C: 的短轴端点,点M在椭圆上运动,且点M不与A1 , A2重合,点N满足NA1⊥MA1 , NA2⊥MA2 , 则 =( ) A、2 B、3 C、4 D、
A、2 B、3 C、4 D、 12. 已知关于 的不等式 有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数 的取值范围是( )A、(
12. 已知关于 的不等式 有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数 的取值范围是( )A、( ,
, 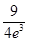 ]
B、(
]
B、( 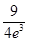 ,
, 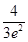 ]
C、[
]
C、[  ,
, 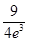 )
D、[
)
D、[ 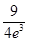 ,
, 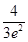 )
)
二、填空题
-
13. 已知向量 , 间的夹角为 ,若 , ,则 .14. 已知实数x,y满足 则z=x-2y的最大值为 .15. 的展开式中,含 项的系数为 .16. 在 中,若 , ,则 面积的最大值为 .
三、解答题
-
17. 已知△ABC中,B= ,AB=4.(1)、若 = ,AD= BD,求BC的长;(2)、若AC=6,求sinC、sin∠BAC的值.18. 已知等差数列 的前n项和为 ,且 , 首项为1的数列 满足 .(1)、求数列 的通项公式及其前n项和 ;(2)、求数列 的前n项和 .19. 为了调查一款电视机的使用时间,研究人员对该款电视机进行了相应的测试,将得到的数据统计如图所示:
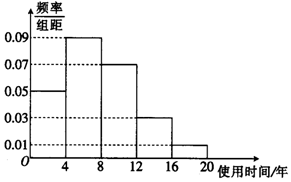
并对不同年龄层的市民对这款电视机的购买意愿作出调查,得到的数据如表所示:
愿意购买该款电视机
不愿意购买该款电视机
总计
40岁以上
______
______
1000
40岁以下
______
600
______
总计
1200
______
______
(1)、根据图中的数据,试估计该款电视机的平均使用时间;(2)、根据表中数据,判断是否有 的把握认为“愿意购买该款电视机”与“市民的年龄”有关;(3)、用频率估计概率,若在该电视机的生产线上随机抽取4台,记其中使用时间不低于4年的电视机的台数为X,求X的分布列及期望.k
附: