山东省邹城市2018-2019学年高三上学期理数期中质量监测试卷
试卷更新日期:2019-01-08 类型:期中考试
一、单选题
-
1. 已知集合 , ,则 =( )A、
 B、
B、 C、
C、 D、
D、 2. 函数 的定义域为( )A、
2. 函数 的定义域为( )A、 B、
B、 C、
C、 D、
D、 3. 设 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 已知 , , ,则有( )A、
3. 设 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 已知 , , ,则有( )A、 B、
B、 C、
C、 D、
D、 5. 定积分 =( )A、
5. 定积分 =( )A、 B、
B、 C、
C、 D、
D、 6. 已知 , ,则 与 的夹角为( )A、 B、
6. 已知 , ,则 与 的夹角为( )A、 B、 C、
D、
7. 已知命题 存在实数 ,满足 ;
C、
D、
7. 已知命题 存在实数 ,满足 ;命题 : ( ).
则下列命题为真命题的是( )
A、 B、
B、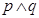 C、
C、 D、
D、 8. 设函数 ( 是常数, ),且函数 的部分图象如图所示,则有( )
8. 设函数 ( 是常数, ),且函数 的部分图象如图所示,则有( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 下图是函数 的部分图象,则函数 的零点所在的区间是( )
9. 下图是函数 的部分图象,则函数 的零点所在的区间是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 已知 ,且 则目标函数 的最小值为( )A、
10. 已知 ,且 则目标函数 的最小值为( )A、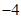 B、
B、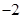 C、
C、 D、
D、 11. 已知 是 的外心, , ,则 ( )A、 B、
11. 已知 是 的外心, , ,则 ( )A、 B、 C、
C、 D、
D、 12. 若直线 是曲线 的切线,也是曲线 的切线,则实数 的值是( )A、
12. 若直线 是曲线 的切线,也是曲线 的切线,则实数 的值是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 已知向量 若 ,则实数 .14. 设当 时,函数 取得最大值,则 .15. 观察下列各式:
… … …
照此规律,则第 个等式应为.
16. 已知函数 是定义在 上的偶函数,其导函数为 ,且当 时, ,则不等式 的解集为.三、解答题
-
17. 设命题 函数 在区间 上单调递减;命题 函数 的值域是 .如果命题 为真命题, 为假命题,求实数 的取值范围.18. 已知向量 , .
(Ⅰ)若 ,求 的值;
(Ⅱ)令 ,把函数 的图象上每一点的横坐标都缩小为原来的一半(纵坐标不变),再把所得图象沿 轴向右平移 个单位,得到函数 的图象,试求函数 的单调增区间及图象的对称中心.
19. 在 中,内角 所对应的边分别为 ,已知 .(Ⅰ)求 的值;
(Ⅱ)试求 的面积.
20. 已知函数 ,不等式 的解集为 .(Ⅰ)求实数 的值;
(Ⅱ)若关于 的不等式 恒成立,求实数 的取值范围.
21. 山东省于2015年设立了水下考古研究中心,以此推动全省的水下考古、水下文化遗产保护等工作;水下考古研究中心工作站,分别设在位于刘公岛的中国甲午战争博物院和威海市博物馆。为对刘公岛周边海域水底情况进行详细了解,然后再选择合适的时机下水探摸、打捞,省水下考古中心在一次水下考古活动中,某一潜水员需潜水 米到水底进行考古作业,其用氧量包含以下三个方面:①下潜平均速度为 米/分钟,每分钟的用氧量为 升;
②水底作业时间范围是最少10分钟最多20分钟,每分钟用氧量为0.4升;
③返回水面时,平均速度为 米/分钟,每分钟用氧量为0.32升.
潜水员在此次考古活动中的总用氧量为 升.
(Ⅰ)如果水底作业时间是 分钟,将 表示为 的函数;
(Ⅱ)若 ,水底作业时间为20分钟,求总用氧量 的取值范围.
22. 已知函数 ,函数 的图象在 处的切线与直线 平行.(Ⅰ)求实数 的值;
(Ⅱ)若函数 存在单调递减区间,求实数 的取值范围;
(Ⅲ)设 ( )是函数 的两个极值点,若 ,试求 的最小值.