2016-2017学年河南省济源市轵城镇八年级上学期期中数学试卷
试卷更新日期:2017-04-10 类型:期中考试
一、选择题
-
1. 下列平面图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 以下列各组线段为边,能组成三角形的是( )A、1,2,3 B、2,3,5 C、4,6,8 D、5,6,123. 以下是四位同学在钝角三角形ABC中画BC边上的高,其中画法正确的是( )A、
2. 以下列各组线段为边,能组成三角形的是( )A、1,2,3 B、2,3,5 C、4,6,8 D、5,6,123. 以下是四位同学在钝角三角形ABC中画BC边上的高,其中画法正确的是( )A、 B、
B、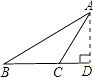 C、
C、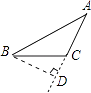 D、
D、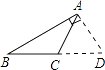 4. 点P(2,﹣3)关于y轴对称点的坐标是( )A、(2,3) B、(﹣2,﹣3) C、(2,﹣3) D、(﹣2,3)5. 十二边形的外角和是( )A、180° B、360° C、1800° D、2160°6. 已知等腰三角形的两边长分别是3和6,则它的周长等于( )A、12 B、12或15 C、15或18 D、157. 如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( )
4. 点P(2,﹣3)关于y轴对称点的坐标是( )A、(2,3) B、(﹣2,﹣3) C、(2,﹣3) D、(﹣2,3)5. 十二边形的外角和是( )A、180° B、360° C、1800° D、2160°6. 已知等腰三角形的两边长分别是3和6,则它的周长等于( )A、12 B、12或15 C、15或18 D、157. 如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( )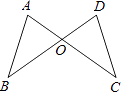 A、AB=DC B、OB=OC C、∠C=∠D D、∠AOB=∠DOC8. 如图所示,AC=BD,AB=CD,图中全等的三角形的对数是( )
A、AB=DC B、OB=OC C、∠C=∠D D、∠AOB=∠DOC8. 如图所示,AC=BD,AB=CD,图中全等的三角形的对数是( ) A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
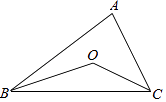
9. 如图,已知点O是△ABC内一点,且点O到三边的距离相等,∠A=40°,则∠BOC= .
 10. 三角形的两边长分别是3和7,则其第三边x的范围为 .11. 如果一个正多边形的内角和是720°,则这个正多边形是正边形.12. 已知在△ABC中,∠A=40°,∠B﹣∠C=40°,则∠B= , ∠C= .13. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= .
10. 三角形的两边长分别是3和7,则其第三边x的范围为 .11. 如果一个正多边形的内角和是720°,则这个正多边形是正边形.12. 已知在△ABC中,∠A=40°,∠B﹣∠C=40°,则∠B= , ∠C= .13. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= . 14. 若等腰三角形腰上的高是腰长的一半,则这个等腰三角形的底角是 .15. 如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是(填写序号).
14. 若等腰三角形腰上的高是腰长的一半,则这个等腰三角形的底角是 .15. 如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是(填写序号).
三、解答题
-
16.
利用关于坐标轴对称的点的坐标的特点,在下面坐标系中作出△ABC关于y轴对称的图形△A′B′C′,并写出A′,B′,C′的坐标.
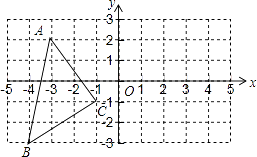 17. 已知:AB=CD,AE⊥BC,DF⊥BC,垂足分别为E、F,AE=DF.求证:AB∥CD.
17. 已知:AB=CD,AE⊥BC,DF⊥BC,垂足分别为E、F,AE=DF.求证:AB∥CD. 18.
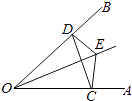
18.某地有两个村庄M、N和两条相交叉的公路OA,OB,现计划修建一个物资仓库,希望仓库到两个村庄的距离相等,到两条公路的距离也相等,请你用尺规作图的方法确定该点P.(注意保留作图痕迹,不用写作法)
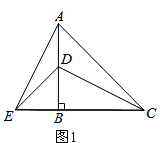
 19. 如图,在△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B.求证:ED=EF.
19. 如图,在△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B.求证:ED=EF.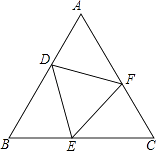 20. 如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
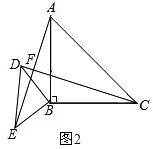
20. 如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.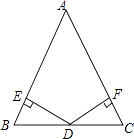 (1)、求证:DE=DF;(2)、若∠A=60°,BE=1,求△ABC的周长.21. 如图,AC=BC,∠CAD=∠BCE,∠ACB=80°,∠E=100°.
(1)、求证:DE=DF;(2)、若∠A=60°,BE=1,求△ABC的周长.21. 如图,AC=BC,∠CAD=∠BCE,∠ACB=80°,∠E=100°.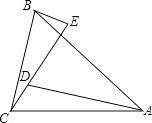 (1)、求证:△ACD≌△CBE;(2)、如果AD=25cm,DE=17cm,求BE的长.
(1)、求证:△ACD≌△CBE;(2)、如果AD=25cm,DE=17cm,求BE的长.