2016-2017学年河北省唐山市路北区八年级上学期期中数学试卷
试卷更新日期:2017-04-10 类型:期中考试
一、选择题
-
1. 下列各式运算正确的是( )A、a2+a3=a5 B、a2•a3=a5 C、(ab2)3=ab6 D、a10÷a2=a52. 下列长度的三条线段,不能组成三角形的是( )A、3,8,4 B、4,9,6 C、15,20,8 D、9,15,83. 点M(﹣3,2)关于y轴对称的点的坐标为( )A、(﹣3,﹣2) B、(3,﹣2) C、(﹣3,2) D、(3,2)4. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、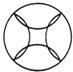 D、
D、 5. 一个等腰三角形的两边长分别为2和5,则它的周长为( )A、7 B、9 C、12 D、9或126. 计算(x﹣6)(x+1)的结果为( )A、x2+5x﹣6 B、x2﹣5x﹣6 C、x2﹣5x+6 D、x2+5x+67. 若|x+y﹣5|+(x﹣y﹣3)2=0,则x2﹣y2的结果是( )A、2 B、8 C、15 D、168. 化简(m2+1)(m+1)(m﹣1)﹣(m4+1)的值是( )A、﹣2m2 B、0 C、﹣1 D、﹣29. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
5. 一个等腰三角形的两边长分别为2和5,则它的周长为( )A、7 B、9 C、12 D、9或126. 计算(x﹣6)(x+1)的结果为( )A、x2+5x﹣6 B、x2﹣5x﹣6 C、x2﹣5x+6 D、x2+5x+67. 若|x+y﹣5|+(x﹣y﹣3)2=0,则x2﹣y2的结果是( )A、2 B、8 C、15 D、168. 化简(m2+1)(m+1)(m﹣1)﹣(m4+1)的值是( )A、﹣2m2 B、0 C、﹣1 D、﹣29. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )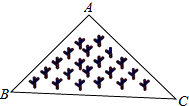 A、△ABC的三条中线的交点 B、△ABC三条角平分线的交点 C、△ABC三条高所在直线的交点 D、△ABC三边的中垂线的交点10. 用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( )
A、△ABC的三条中线的交点 B、△ABC三条角平分线的交点 C、△ABC三条高所在直线的交点 D、△ABC三边的中垂线的交点10. 用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( )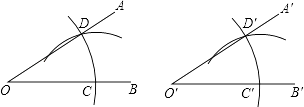 A、(SAS) B、(SSS) C、(ASA) D、(AAS)11. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A、(SAS) B、(SSS) C、(ASA) D、(AAS)11. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )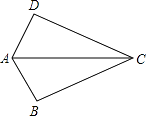 A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、∠B=∠D=90°12. 如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )
A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、∠B=∠D=90°12. 如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )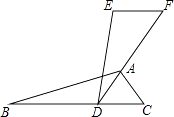 A、50° B、60° C、100° D、120°13. 如图是跷跷板的示意图.支柱OC与地面垂直,点O是横板AB的中点,AB可以绕着点O上下转动,当A端落地时,∠OAC=20°,跷跷板上下可转动的最大角度(即∠A′OA)是( )
A、50° B、60° C、100° D、120°13. 如图是跷跷板的示意图.支柱OC与地面垂直,点O是横板AB的中点,AB可以绕着点O上下转动,当A端落地时,∠OAC=20°,跷跷板上下可转动的最大角度(即∠A′OA)是( )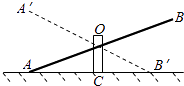 A、80° B、60° C、40° D、20°14.
A、80° B、60° C、40° D、20°14.如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
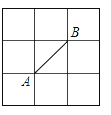 A、6 B、7 C、8 D、9
A、6 B、7 C、8 D、9二、填空题
-
15. 计算:a8÷a5= .16. 若(mx﹣6y)与(x+3y)的积中不含xy项,则m的值为 .17. 如图,△ABC≌△ADE,∠EAC=35°,则∠BAD=°.
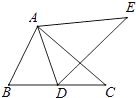 18. 如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=36cm2 , AB=18cm,BC=12cm,则DE=cm.
18. 如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=36cm2 , AB=18cm,BC=12cm,则DE=cm.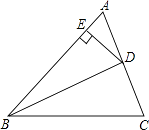
三、解答题
-
19. (﹣64x4y3)÷(﹣2xy)320. 计算:[x(x2y2﹣xy)﹣y(x2﹣x3y)]÷x2y.21. 先化简,再求值:x(x﹣2)﹣(x+1)(x﹣1),其中x=10.22. 红枣丰收了,为了运输方便,小华的爸爸打算把一个长为(a+2b)cm、宽为(a+b)cm的长方形纸板制成一个有底无盖的盒子,在长方形纸板的四个角各截去一个边长为 bcm的小正方形,然后沿折线折起即可,如图所示,现将盒子的外表面贴上彩色花板.
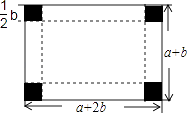 (1)、则至少需要彩纸的面积是多少?(2)、当a=8,b=6时,求至少需要彩纸的面积是多少?23. 如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)、则至少需要彩纸的面积是多少?(2)、当a=8,b=6时,求至少需要彩纸的面积是多少?23. 如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).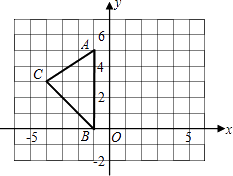 (1)、求出△ABC的面积.(2)、在图中作出△ABC关于y轴的对称图形△A1B1C1 .(3)、写出点A1 , B1 , C1的坐标.24. 如图,E、F是线段BD上的两点,且DF=BE,AE=CF,AE∥CF.
(1)、求出△ABC的面积.(2)、在图中作出△ABC关于y轴的对称图形△A1B1C1 .(3)、写出点A1 , B1 , C1的坐标.24. 如图,E、F是线段BD上的两点,且DF=BE,AE=CF,AE∥CF.求证:AD∥BC.
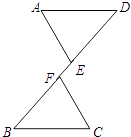 25. 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
25. 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.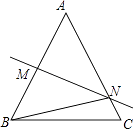 (1)、若∠ABC=70°,则∠MNA的度数是 .(2)、连接NB,若AB=8cm,△NBC的周长是14cm.
(1)、若∠ABC=70°,则∠MNA的度数是 .(2)、连接NB,若AB=8cm,△NBC的周长是14cm.①求BC的长;
②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
26. 四边形ABCD是正方形(提示:正方形四边相等,四个角都是90°)(1)、如图1,若点G是线段CD边上任意一点(不与点C、D重合),连接AG,作BF⊥AG于点F,DE⊥AG于点E,求证:△ABF≌△DAE. (2)、如图2,若点G是线段CD延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,判断线段EF与AF、BF的数量关系,并证明.
(2)、如图2,若点G是线段CD延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,判断线段EF与AF、BF的数量关系,并证明.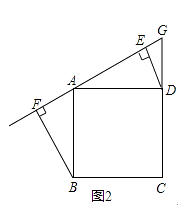 (3)、若点G是直线BC上任意一点(不与点B、C重合),连接AG,作BF⊥AG于点F,DE⊥AG于点E,探究线段EF与AF、BF的数量关系.(请画图、不用证明、直接写答案)
(3)、若点G是直线BC上任意一点(不与点B、C重合),连接AG,作BF⊥AG于点F,DE⊥AG于点E,探究线段EF与AF、BF的数量关系.(请画图、不用证明、直接写答案)