2016-2017学年广西玉林市博白县八年级上学期期中数学试卷
试卷更新日期：2017-04-10 类型：期中考试
一、选择题
-
1. 三角形的内角和等于（ ）A、90° B、180° C、300° D、360°2. 下列图形中，是轴对称图形的是（ ）A、
B、
C、
D、
3. 若一个三角形的两边长分别为3和6，则第三边长可能是（ ）A、6 B、3 C、2 D、104. 下列图形中具有稳定性的是（ ）A、正三角形 B、正方形 C、正五边形 D、正六边形5. 若△ABC中，∠A：∠B：∠C=1：2：3，则△ABC一定是（ ）A、锐角三角形 B、钝角三角形 C、直角三角形 D、任意三角形6. 在Rt△ABC中，∠C=90°，∠B=30°，斜边AB的长为2，则AC长为（ ）A、4 B、2 C、1 D、7. 下列说法正确的是（ ）A、形状相同的两个三角形全等 B、面积相等的两个三角形全等 C、完全重合的两个三角形全等 D、所有的等边三角形全等8. 用直尺和圆规作已知角的平分线的示意图如右，则说明∠CAD=∠DAB的依据是（ ）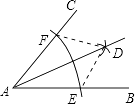
A、SSS B、SAS C、ASA D、AAS9. 根据下列已知条件，能唯一画出△ABC的是（ ）A、AB=3，BC=4，AC=8 B、∠C=90°，AB=6 C、∠A=60°，∠B=45°，AB=4 D、AB=3，BC=3，∠A=30°10. 如图，在等腰三角形纸片ABC中，AB=AC，∠A=40°，折叠该纸片，使点A落在点B处，折痕为DE，则∠CBE的度数是（ ）
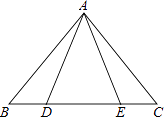
A、20° B、30° C、40° D、70°11. 如图，在△ABC中，AB=AC，∠A=30°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D的度数为（ ）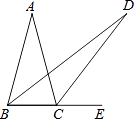
A、15° B、17.5° C、20° D、22.5°12. 如图，等腰三角形ABC中，AB=AC，D、E都在BC上，要使△ABD≌△ACE，需要添加一个条件，某学习小组在讨论这个条件时给出了如下几种方案：①AD=AE；②BD=CE；③BE=CD；④∠BAD=∠CAE，其中可行的有（ ）
A、1种 B、2种 C、3种 D、4种二、填空题
-
13. 点P（﹣2，3）关于y轴对称的点的坐标是 ．14. 等腰三角形的一个内角为100°，则它的底角为 ．15. 若一个多边形外角和与内角和相等，则这个多边形是边形．16. 如图，已知AB=AD，∠BAE=∠DAC，要使△ABC≌△ADE，若以“SAS”为依据，补充的条件是 ．
17. 如图，在△ABC中，∠C=90°，AD平分∠BAC，BC=12cm，BD=9cm，则点D到AB的距离是 cm．
18. 如图，在△ABC中，∠ACB=90°，∠ABC=60°，BD平分∠ABC，P点是BD的中点，若AD=8，则CP的长为 ．
三、解答题
-
19. 一个多边形的内角和是它的外角和的4倍，求这个多边形的边数．20. 已知：如图，AB=AC，DB=DC，求证：∠B=∠C．
21. 如图，△ABC与△ADE关于直线MN对称，BC与DE的交点F在直线MN上．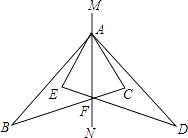
(1)、图中点B的对称点是 ， 点C的对称点是；(2)、写出图中相等的一对线段是 ， 相等的一对角是；(3)、写出图中全等的一对三角形是 ．22. 如图，在△ABC中，∠B=40°，∠C=70°，AD是△BAC的角平分线，求∠ADC的度数．
23. 已知：如图，CE⊥AB，BF⊥AC，CE与BF相交于D，且BD=CD．求证：D在∠BAC的平分线上．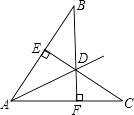
24. 如图，已知AB=CD，∠B=∠C，AC和BD相交于点O，E是AD的中点，连接OE．
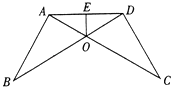(1)、求证：△AOB≌△DOC；(2)、求∠AEO的度数．
