2016-2017学年广西柳州市柳江县八年级上学期期中数学试卷
试卷更新日期：2017-04-10 类型：期中考试
一、选择题
-
1. 在以下大众、东风、长城、奔驰四个汽车标志中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 平面内点A（﹣1，2）和点B（﹣1，﹣2）的对称轴是（ ）A、x轴 B、y轴 C、直线y=4 D、直线x=﹣13. 在△ABC中，∠A=30°，∠B=50°，则∠C为（ ）A、30° B、50° C、80° D、100°4. 下列图形中对称轴最多的是（ ）A、等腰三角形 B、正方形 C、圆形 D、线段5. 以下列各组线段长为边，能组成三角形的是（ ）A、1cm，2cm，4cm B、8cm，6cm，4cm C、12cm，5cm，6cm D、2cm，3cm，6cm6. 如图所示，∠B=∠D=90°，BC=CD，∠1=40°，则∠2=（ ）
A、40° B、50° C、45° D、60°7. 如图所示，某同学把一块三角形的玻璃不小心打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带（ ）去．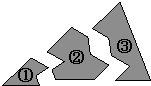
A、① B、② C、③ D、①和②8.把一个正方形三次对折后沿虚线剪下，如图所示，则所得的图形是（ ）
A、
B、
C、
D、
9. △ABC中，AB=AC，AB的垂直平分线与直线AC相交所成锐角为40°，则此等腰三角形的顶角为（ ）A、50° B、60° C、150° D、50°或130°10. 如图，已知MB=ND，∠MBA=∠NDC，下列条件中不能判定△ABM≌△CDN的是（ ）
A、∠M=∠N B、AM=CN C、AB=CD D、AM∥CN二、填空题
-
11. 点P（1，﹣1）关于x轴对称的点的坐标为P′ ．12. 五边形的内角和为 ．13.
小明从平面镜子中看到镜子对面电子钟示数的像如图所示，这时的时刻应是 ．
14. 如图，已知AD=BC，根据“SSS”，还需要一个条件 ， 可证明△ABC≌△BAD；根据“要SAS”，还需要一个条件 ， 可证明△ABC≌△BAD．
15. 已知CD垂直平分AB，若AC=4cm，AD=5cm，则四边形ADBC的周长是 cm．
16. 如图所示，∠B=∠D=90°，要证明△ABC与△ADC全等，还需要补充的条件是 ． （填上一个条件即可）
三、解答题
-
17.
作图：
①如图1，作出∠AOB的角平分线OC，不写作法但要保留作图痕迹．
②如图2，把下列图形补成关于L对称的图形（保留痕迹）
18.要在燃气管道L上修建一个泵站P，分别向A，B两镇供气，泵站修在管道的什么地方，可使所用的输气管线最短？在图上画出P点位置，保留作图痕迹．
19.如图，写出△ABC的各顶点坐标，并画出△ABC关于y轴对称的△A1B1C1 ， 写出△ABC关于X轴对称的△A2B2C2的各点坐标．
20. 如图，点E，F在BC上，BE=CF，∠A=∠D，∠B=∠C，AF与DE交于点O．
(1)、求证：AB=DC；(2)、试判断△OEF的形状，并说明理由．21. 如图，点P在AB上，∠1=∠2，∠3=∠4，求证：AC=AD．
22. 如图，已知：△ABC中，AB=AC，BD和CE分别是∠ABC和∠ACB的角平分线，且相交于O点．①试说明△OBC是等腰三角形；
②连接OA，试判断直线OA与线段BC的关系，并说明理由．
23.八（3）班同学到野外上数学活动课，为测量池塘两端A、B的距离，设计了如下方案：
（Ⅰ）如图1，先在平地上取一个可直接到达A、B的点C，连接AC、BC，并分别延长AC至D，BC至E，使DC=AC，EC=BC，最后测出DE的距离即为AB的长；
（Ⅱ）如图2，先过B点作AB的垂线，再在BF上取C、D两点使BC=CD，接着过D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离．
阅读回答下列问题：
(1)、方案（Ⅰ）是否可行？请说明理由．(2)、方案（Ⅱ）是否可行？请说明理由．(3)、方案（Ⅲ）中作BF⊥AB，ED⊥BF的目的是；若仅满足∠ABD=∠BDE≠90°，方案（Ⅱ）是否成立？ ．