2016-2017学年广西贵港市港南区八年级上学期期中数学试卷

试卷更新日期：2017-04-10 类型：期中考试

进入出卷网下载

一、选择题

1. 下列各式： $\frac{a - b}{2}$ ， $\frac{x + 3}{x}$ ， $\frac{5 + y}{π}$ ， $\frac{a + b}{a - b}$ ， $\frac{1}{m}$ （x+y）中，是分式的共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 点M（1，2）关于x轴对称的点的坐标为（　　）

A、（﹣1，﹣2） B、（﹣1，2） C、（1，﹣2） D、（2，﹣1）

查看试题解析
3. 如果D是△ABC中BC边上一点，并且△ADB≌△ADC，则△ABC是（　　）

A、锐角三角形 B、钝角三角形 C、直角三角形 D、等腰三角形

查看试题解析
4. 分式﹣ $\frac{1}{1 - x}$ 可变形为（）

A、 $\frac{1}{x + 1}$ B、 $\frac{1}{1 - x}$ C、﹣ $\frac{1}{x - 1}$ D、 $\frac{1}{x - 1}$

查看试题解析
5. 若等腰三角形的周长为26cm，一边为11cm，则腰长为（　　）

A、11cm B、7.5cm C、11cm或7.5cm D、以上都不对

查看试题解析
6. 若等腰三角形一腰上的高是腰长的一半，则这个等腰三角形的底角是（）

A、75°或15° B、75° C、15° D、75°或30°

查看试题解析
7. 若分式 $\frac{x^{2} - 1}{x + 1}$ 的值为零，那么x的值为（）

A、x=﹣1或x=1 B、x=0 C、x=1 D、x=﹣1

查看试题解析
8. 若等腰三角形中有两边长分别为2和5，则这个三角形的周长为（）

A、9 B、12 C、7或9 D、9或12

查看试题解析
9. 如图，已知MB=ND，∠MBA=∠NDC，下列条件中不能判定△ABM≌△CDN的是（）

A、∠M=∠N B、AM=CN C、AB=CD D、AM∥CN

查看试题解析
10. 如图，在△ABC中，∠B=46°，∠C=54°，AD平分∠BAC，交BC于D，DE∥AB，交AC于E，则∠ADE的大小是（）

A、45° B、54° C、40° D、50°

查看试题解析
11. 如图所示，在△ABC中，AB=AC，D、E是△ABC内两点，AD平分∠BAC．∠EBC=∠E=60°，若BE=6，DE=2，则BC的长度是（）

A、6 B、8 C、9 D、10

查看试题解析
12. 如图，在△ABC中，∠A=36°，AB=AC，BD是△ABC的角平分线．若在边AB上截取BE=BC，连接DE，则图中等腰三角形共有（）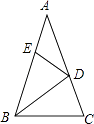

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

13. 如果分式 $\frac{2 x}{x + 3}$ 有意义，那么x的取值范围是．

查看试题解析
14. 一个正数的平方根是2a﹣1和3﹣a，则这个正数是．

查看试题解析
15. 若解分式方程 $\frac{x - 1}{x + 4} = \frac{m}{x + 4}$ 产生增根，则m= ．

查看试题解析
16. 如图，在△ABC中，AB=AC，点E在CA延长线上，EP⊥BC于点P，交AB于点F，若AF=2，BF=3，则CE的长度为．

查看试题解析
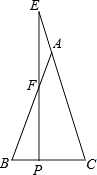17. 如图，△ABC中，∠A=90°，DE是BC的垂直平分线，AD=DE，则∠C的度数是°．

查看试题解析
18. 如图，在△ABC中，AB=1.8，BC=3.9，∠B=60°，将△ABC绕点A按顺时针旋转一定角度得到△ADE，当点B的对应点D恰好落在BC边上时，则CD的长为．

查看试题解析

三、解答题

19. 计算下面各题

(1)、计算：（﹣ $\frac{1}{2}$ ）^﹣¹﹣2+（π﹣3.14）⁰

(2)、解方程： $\frac{3}{x}$ = $\frac{2}{x - 1}$ ．

查看试题解析
20. 一个多边形的内角和是它的外角和的4倍，求这个多边形的边数．

查看试题解析
21. 作图题

(1)、
如图，已知△ABC，请你作出AB边上的高CD，AC边上的中线BE，角平分线AF（不写作法，保留痕迹）

(2)、
如图，直线l表示一条公路，点A，点B表示两个村庄．现要在公路上造一个车站，并使车站到两个村庄A，B的距离之和最短，问车站建在何处？请在图上标明地点，并说明理由．（要求尺规作图，不写作法）

查看试题解析
22. 已知x+y=﹣4，xy=﹣12，求 $\frac{y + 1}{x + 1} + \frac{x + 1}{y + 1}$ 的值．

查看试题解析
23. 李明到离家2.1千米的学校参加初三联欢会，到学校时发现演出道具还放在家中，此时距联欢会开始还有42分钟，于是他立即匀速步行回家，在家拿道具用了1分钟，然后立即匀速骑自行车返回学校．已知李明骑自行车到学校比他从学校步行到家用时少20分钟，且骑自行车的速度是步行速度的3倍．

(1)、李明步行的速度（单位：米/分）是多少？

(2)、李明能否在联欢会开始前赶到学校？

查看试题解析
24. 在△ABC中，AB＞BC，AB=AC，DE是AB的垂直平分线，垂足为D，交AC于E．

(1)、若∠ABE=40°，求∠EBC的度数；

(2)、若△ABC的周长为41cm，一边长为15cm，求△BCE的周长．

查看试题解析
25. 观察下面的变形规律：
$\frac{1}{1 \times 2}$ =1﹣ $\frac{1}{2}$ ； $\frac{1}{2 \times 3}$ = $\frac{1}{2}$ ﹣ $\frac{1}{3}$ ； $\frac{1}{3 \times 4}$ = $\frac{1}{3}$ ﹣ $\frac{1}{4}$ ；…解答下面的问题：

(1)、若n为正整数，请你猜想 $\frac{1}{n (n + 1)}$ =；

(2)、求和： $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ ．（注：只能用上述结论做才能给分）；

(3)、用上述相似的方法求和： $\frac{1}{1 \times 3}$ + $\frac{1}{3 \times 5}$ + $\frac{1}{5 \times 7}$ +…+ $\frac{1}{2013 \times 2015}$ ．

查看试题解析
26. 已知如图1：△ABC中，AB=AC，∠B、∠C的平分线相交于点O，过点O作EF∥BC交AB、AC于E、F．

(1)、图中有几个等腰三角形？请说明EF与BE、CF间有怎样的关系．

(2)、若AB≠AC，其他条件不变，如图2，图中还有等腰三角形吗？如果有，请分别指出它们．另第（1）问中EF与BE、CF间的关系还存在吗？

(3)、若△ABC中，∠B的平分线与三角形外角∠ACD的平分线CO交于O，过O点作OE∥BC交AB于E，交AC于F．如图3，这时图中还有哪几个等腰三角形？EF与BE、CF间的关系如何？为什么？

查看试题解析