2016-2017学年广西防城港市八年级上学期期中数学试卷
试卷更新日期:2017-04-10 类型:期中考试
一、选择题
-
1. 在△ABC中,∠A=40°,∠B=60°,则∠C=( )A、40° B、80° C、60° D、100°2. 下列能组成三角形的线段是( )A、3cm、3cm、6cm B、3cm、4cm、5cm C、2cm、4cm、6cm D、3cm、5cm、9cm3. 若等腰三角形的顶角为80°,则它的底角度数为( )A、80° B、50° C、40° D、20°4. 点M(1,﹣2)关于y轴的对称点坐标为( )A、(﹣1,2) B、(2,﹣1) C、(1,2) D、(﹣1,﹣2)5. 如图所示的标志中,是轴对称图形的有( )
 A、1个 B、2个 C、3个 D、4个6. 下列各图中,正确画出AC边上的高的是( )A、
A、1个 B、2个 C、3个 D、4个6. 下列各图中,正确画出AC边上的高的是( )A、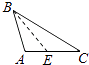 B、
B、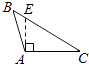 C、
C、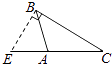 D、
D、 7. 三角形中,到三边距离相等的点是( )A、三条角平分线的交点 B、三边垂直平分线的交点 C、三条高线的交点 D、三条中线的交点8. 如图,已知△ADB≌△CBD,AB=4,BD=6,BC=3,则△ADB的周长是( )
7. 三角形中,到三边距离相等的点是( )A、三条角平分线的交点 B、三边垂直平分线的交点 C、三条高线的交点 D、三条中线的交点8. 如图,已知△ADB≌△CBD,AB=4,BD=6,BC=3,则△ADB的周长是( )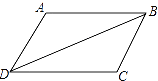 A、12 B、13 C、14 D、159.
A、12 B、13 C、14 D、159.如图所示,在Rt△ACB中,∠C=90°,AD平分∠BAC,若BC=16,BD=10,则点D到AB的距离是( )
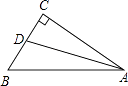 A、9 B、8 C、7 D、610. 如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
A、9 B、8 C、7 D、610. 如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )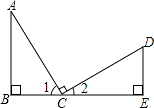 A、AC=BC+CE B、∠A=∠2 C、△ABC≌△CED D、∠A与∠D互余11. 如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )
A、AC=BC+CE B、∠A=∠2 C、△ABC≌△CED D、∠A与∠D互余11. 如图所示,AD=AE,BD=CE,∠ADB=AEC=100°,∠BAE=70°,下列结论错误的是( )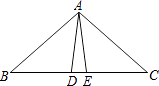 A、△ABE≌△ACD B、△ABD≌△ACE C、∠C=30° D、∠DAE=40°
A、△ABE≌△ACD B、△ABD≌△ACE C、∠C=30° D、∠DAE=40°二、填空题
-
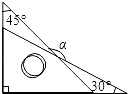
12. 把一副三角板按如图方式放置,则两条斜边所形成的钝角α=度.
 13. 如图,已知∠1=100°,∠2=140°,那么∠3=度.
13. 如图,已知∠1=100°,∠2=140°,那么∠3=度.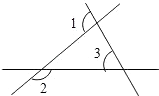 14. 已知等腰三角形的两边长分别为5cm和8cm,且它的周长大于19cm,则第三边长为15. 点O是△ABC内一点,且点O到三边的距离相等,∠A=60°,则∠BOC的度数为 .16. 如图是一个三角形测平架,已知AB=AC,在BC的中点D挂一个重锤DE,让其自然下垂,调整架身,使点A恰好在重锤线上,这时AD和BC的位置关系为
14. 已知等腰三角形的两边长分别为5cm和8cm,且它的周长大于19cm,则第三边长为15. 点O是△ABC内一点,且点O到三边的距离相等,∠A=60°,则∠BOC的度数为 .16. 如图是一个三角形测平架,已知AB=AC,在BC的中点D挂一个重锤DE,让其自然下垂,调整架身,使点A恰好在重锤线上,这时AD和BC的位置关系为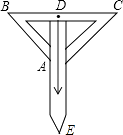 17. 一个多边形的内角和等于1080°,这个多边形是边形.18. 点A(﹣2a,a﹣1)在x轴上,则A点的坐标是 , A点关于y轴的对称点的坐标是 .19. 如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为 .
17. 一个多边形的内角和等于1080°,这个多边形是边形.18. 点A(﹣2a,a﹣1)在x轴上,则A点的坐标是 , A点关于y轴的对称点的坐标是 .19. 如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为 .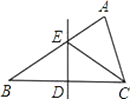
三、解答题
-
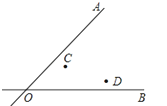
20.
如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修建一个货站P,使货站P到两条公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)
 21. 已知:如图,A、F、C、D四点在一直线上,AF=CD,AB∥DE,且AB=DE.
21. 已知:如图,A、F、C、D四点在一直线上,AF=CD,AB∥DE,且AB=DE.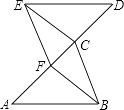
求证:
(1)、△ABC≌△DEF;
(2)、BC∥EF.
22. 如图,△ABC的边BC上的高为AF,AC边上的高为BG,中线为AD,已知AF=6,BC=10,BG=5.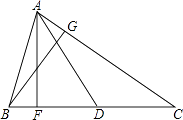 (1)、求△ABC的面积;(2)、求AC的长;(3)、试说明△ABD和△ACD的面积相等.23. 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)、求△ABC的面积;(2)、求AC的长;(3)、试说明△ABD和△ACD的面积相等.23. 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.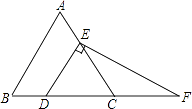 (1)、求∠F的度数;(2)、若CD=2,求DF的长.24.
(1)、求∠F的度数;(2)、若CD=2,求DF的长.24.如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
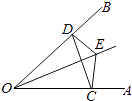
求证:
(1)、∠ECD=∠EDC;
(2)、OC=OD
(3)、OE是线段CD的垂直平分线.
25. 如图,已知△ABC中,∠B=∠C,AB=8厘米,BC=6厘米,点D为AB的中点.如果点P在线段BC上以每秒2厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).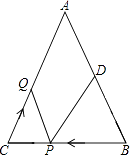 (1)、用的代数式表示PC的长度;(2)、若点P、Q的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;(3)、若点P、Q的运动速度不相等,当点Q的运动速度a为多少时,能够使△BPD与△CQP全等?
(1)、用的代数式表示PC的长度;(2)、若点P、Q的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;(3)、若点P、Q的运动速度不相等,当点Q的运动速度a为多少时,能够使△BPD与△CQP全等?