山东省潍坊市2018-2019学年高三上学期数学期中考试试卷
试卷更新日期:2019-01-08 类型:期中考试
一、单选题
-
1. 已知集合 ( )A、
 B、
B、 C、
C、 D、
D、 2. 已知命题 ,那么 是( )A、
2. 已知命题 ,那么 是( )A、 B、
B、 C、
C、 D、
D、 3. 下列说法正确的是( )A、若
3. 下列说法正确的是( )A、若 ,则
,则  B、若
B、若 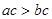 ,则
,则 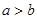 C、若
C、若 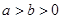 ,则
,则 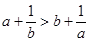 D、若
D、若 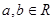 ,则
,则 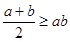 4. 若曲线 在点(1,m)处的切线垂直于y轴,则实数 ( )A、
4. 若曲线 在点(1,m)处的切线垂直于y轴,则实数 ( )A、 B、0
C、1
D、2
5. 若 满足约束条件 的最大值为( )A、
B、0
C、1
D、2
5. 若 满足约束条件 的最大值为( )A、 B、0
C、
B、0
C、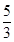 D、
D、 6. 已知偶函数 在 上单调递增,且 ,则满足 的x的取值范围是( )A、
6. 已知偶函数 在 上单调递增,且 ,则满足 的x的取值范围是( )A、 B、[0,2]
C、[1,2]
D、[1,3]
7. 在△ABC中,D为AC的中点,E为线段CB上靠近B的三等分点,则 ( )A、
B、[0,2]
C、[1,2]
D、[1,3]
7. 在△ABC中,D为AC的中点,E为线段CB上靠近B的三等分点,则 ( )A、 B、
B、 C、
C、 D、
D、 8. 已知 为第二象限的角, ,则 的值为( )A、
8. 已知 为第二象限的角, ,则 的值为( )A、 B、
B、 C、
C、 D、
D、 9. 函数 的图象大致为( )A、
9. 函数 的图象大致为( )A、 B、
B、 C、
C、 D、
D、 10. 设l,m表示空间中不同的直线, 表示不同的平面,则下列结论正确的是( )A、若
10. 设l,m表示空间中不同的直线, 表示不同的平面,则下列结论正确的是( )A、若 ,则
,则  B、若
B、若  ,则
,则  C、若
C、若  ,则
,则  D、若
D、若  ,则
,则  11. 鲁班锁是中国传统的智力玩具,起源于中国古代建筑中首创的榫卯结构,它的外观是如图所示的十字立方体,其上下、左右、前后完全对称,六根完全一样的正四棱柱体分成三组,经90°榫卯起来.若正四棱柱的高为5,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积至少为(容器壁的厚度忽略不计) ( )
11. 鲁班锁是中国传统的智力玩具,起源于中国古代建筑中首创的榫卯结构,它的外观是如图所示的十字立方体,其上下、左右、前后完全对称,六根完全一样的正四棱柱体分成三组,经90°榫卯起来.若正四棱柱的高为5,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积至少为(容器壁的厚度忽略不计) ( ) A、
A、 B、
B、 C、
C、 D、
D、 12. 已知函数 ,若存在实数b使函数 有两个零点,则实数a的取值范围是( )A、(0,1) B、(1,+∞) C、(1,2019) D、[1,+∞)
12. 已知函数 ,若存在实数b使函数 有两个零点,则实数a的取值范围是( )A、(0,1) B、(1,+∞) C、(1,2019) D、[1,+∞)二、填空题
-
13. 已知 是夹角为 的两个单位向量, ,则 = .14. 某几何体的三视图如图所示,左视图为半圆,俯视图为等腰三角形,则该几何体的体积为.
 15. 设函数 的部分图象如图所示,若 是边长为2的等边三角形,则 = .
15. 设函数 的部分图象如图所示,若 是边长为2的等边三角形,则 = . 16. 已知偶函数 满足 ,且当 时 .若 时, 有3个零点,则实数 的取值范围为.
16. 已知偶函数 满足 ,且当 时 .若 时, 有3个零点,则实数 的取值范围为.三、解答题
-
17. 已知集合 ;设 ,若 是 的充分不必要条件,求实数 的取值范围.18. 如图
 图1
图1  图2
图2如图1,菱形ABCD中,AB=4,∠A=60°,对角线AC、BD相交于点O.以对角线BD为折痕把△ABD折起,使点A到达如图2所示点E的位置,使∠EOC=60°.
(1)、求证:BD⊥EC;(2)、求三棱锥B—OEC的体积.19. 已知向量 ,函数 ,且 图象经过点 .(1)、求 的值;(2)、求 在 上的单调递减区间.20. △ABC的内角A,B,C的对边分别为 ,已知 且 . (1)、求角 ;(2)、如图,D为△ABC外一点,若在平面四边形ABCD中, ,求△ACD面积的最大值.21. 某公司的新能源产品上市后在国内外同时销售,已知第一批产品上市销售40天内全部售完,该公司对这批产品上市后的国内外市场销售情况进行了跟踪调查,如图所示,其中图①中的折线表示的是国外市场的日销售量与上市时间的关系;图②中的抛物线表示的是国内市场的日销售量与上市时间的关系;下表表示的是产品广告费用、产品成本、产品销售价格与上市时间的关系.
(1)、求角 ;(2)、如图,D为△ABC外一点,若在平面四边形ABCD中, ,求△ACD面积的最大值.21. 某公司的新能源产品上市后在国内外同时销售,已知第一批产品上市销售40天内全部售完,该公司对这批产品上市后的国内外市场销售情况进行了跟踪调查,如图所示,其中图①中的折线表示的是国外市场的日销售量与上市时间的关系;图②中的抛物线表示的是国内市场的日销售量与上市时间的关系;下表表示的是产品广告费用、产品成本、产品销售价格与上市时间的关系. 图① 图②
图① 图② 
第t天产品广告费用(单位:万元)
每件产品成本(单位:万元)
每件产品销售价格(单位:万元)
3
6
10
3
5
(1)、分别写出国外市场的日销售量 、国内市场的日销售量 与产品上市时间t的函数关系式;(2)、产品上市后的哪几天,这家公司的日销售利润超过260万元?(日销售利润=(单件产品销售价-单件产品成本)×日销售量-当天广告费用, )
22. 已知函数 , .(1)、对 , 恒成立,求实数a的取值范围;(2)、当 时,求 在 上的最大值和最小值;(3)、证明:对 都有 成立.