2016-2017学年福建省莆田市仙游县郊尾、枫亭五校教研小片区八年级上学期期中数学试卷
试卷更新日期：2017-04-10 类型：期中考试
一、精心选一选
-
1. 下列图形是轴对称图形的有（ ）
A、2个 B、3个 C、4个 D、5个2. 等腰三角形两边长分别为4和8，则这个等腰三角形的周长为（ ）A、16 B、18 C、20 D、16或203. 下列图形中具有稳定性的是（ ）A、等边三角形 B、正方形 C、平行四边形 D、梯形4. 在△ABC中，∠A= ∠B= ∠C，则此三角形是（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形5. 如图，在△ABC中，AB=AC，BE、CF是中线，则由（ ）可得△AFC≌△AEB．
A、SSS B、SAS C、AAS D、ASA6. 如图，AE⊥BC于E，BF⊥AC于F，CD⊥AB于D，则△ABC中AC边上的高是哪条垂线段（ ）
A、BF B、CD C、AE D、AF7. 若一个多边形共有20条对角线，则它是（ ）边形．A、六 B、七 C、八 D、九8. 如图在△ABC中，M是BC的中点，S△ABC=16，则S△ABM是（ ）
A、12 B、8 C、6 D、49. 能说明△ABC≌△DEF的条件是（ ）A、AB=DE，AC=DF，∠C=∠F B、AC=EF，∠A=∠D，∠B=∠E C、AB=DE，BC=EF，∠A=∠D D、BC=EF，AB=DE，∠B=∠E10. 在△ABC中，∠A=55°，∠B比∠C大25°，则∠B的度数为（ ）A、125° B、100° C、75° D、50°二、细心填一填
-
11. 已知点P（﹣3，4），关于x轴对称的点的坐标为 ．12. 已知一个多边形的内角和是外角和的2倍，此多边形是 边形．13. 已知△ABC≌△DEF，且△ABC的周长为12，若AB=3，EF=4，则AC= ．14. 如图所示，∠CAB的外角等于120°，∠B等于40°，则∠C的度数是 ．
15. 如图为6个边长等的正方形的组合图形，则∠1+∠2+∠3=°．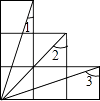
16. 如图，点P在∠AOB的内部，点M、N分别是点P关于直线OA、OB的对称点，线段MN交OA、OB于点E、F，若△PEF的周长是30cm，则线段MN的长是 ．
三、耐心做一做
-
17. 如图，∠1=∠2，∠C=∠D，求证：AC=AD．
18. 如图：已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F．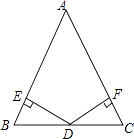
(1)、求证：DE=DF；(2)、若∠A=60°，BE=1，求△ABC的周长．19.如图，在平面直角坐标系中，A（﹣1，5）、B（﹣1，0）、C（﹣4，3）．
(1)、在图中作出△ABC关于y轴的对称图形△A1B1C1 ．(2)、写出点A1、B1、C1的坐标．20. 已知：如图，点D、E在BC上，且BD=CE，AD=AE，求证：AB=AC．
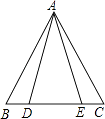21. 在三角形ABC中，∠A=80°，OB、OC分别平分∠ABC和∠ACB，你能求出∠BOC的度数．22. 如图，△ABC中，∠ACB=90°，AC=BC，AE是BC边上的中线，过C作CF⊥AE，垂足为F，过B作BD⊥BC交CF的延长线于D．
(1)、求证：AE=CD；(2)、若AC=12cm，求BD的长．23. 如图所示，在△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠BAC=60°，∠C=70°，求∠DAE、∠BOA的度数．
24. 已知：如图，点E在AC上，点F在AB上，BE，CF交于点O，且∠C=2∠B，∠BFC比∠BEC大20°，求∠C的度数．
25. 如图，点E，F在BC上，BE=CF，∠A=∠D，∠B=∠C，AF与DE交于点O．
(1)、求证：AB=DC；(2)、试判断△OEF的形状，并说明理由．26. 如图1，在平面直角坐标系中，△AOB为等腰直角三角形，A（4，4）
(1)、求B点坐标；(2)、如图2，若C为x轴正半轴上一动点，以AC为直角边作等腰直角△ACD，∠ACD=90°连OD，求∠AOD的度数；
(3)、如图3，过点A作y轴的垂线交y轴于E，F为x轴负半轴上一点，G在EF的延长线上，以EG为直角边作等腰Rt△EGH，过A作x轴垂线交EH于点M，连FM，等式AM=FM+OF是否成立？若成立，请证明：若不成立，说明理由．