浙江省湖州市长兴县2018-2019学年九年级上学期数学第三次月考试卷
试卷更新日期:2019-01-05 类型:月考试卷
一、选择题。
-
1. 抛物线y=(x-2)2的对称轴是( )A、直线x=-1 B、直线x=1 C、直线x=-2 D、直线x=22. 如图。已知点A,B,C在圆O上.若∠ACB=50°,则∠AOB的度数是( )
 A、100° B、1050° C、110° D、130°3. 将抛物线y=x2向上平移两个单位,得到的新抛物线的函数表达式为( )A、y=x2-2 B、y=x2+2 C、y=(z-2)2 D、y=(x+2)24. 如图.已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若再 ,DE=2,则EF的长是( )
A、100° B、1050° C、110° D、130°3. 将抛物线y=x2向上平移两个单位,得到的新抛物线的函数表达式为( )A、y=x2-2 B、y=x2+2 C、y=(z-2)2 D、y=(x+2)24. 如图.已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若再 ,DE=2,则EF的长是( ) A、6 B、5 C、4 D、35. 已知圆O的半径为10,弦AB=16,则圆心O到弦AB的距离是( )A、
A、6 B、5 C、4 D、35. 已知圆O的半径为10,弦AB=16,则圆心O到弦AB的距离是( )A、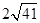 B、
B、 C、12
D、6
6. 有一种纸上游戏叫“划蟹脚”,如图,每个数字连线着一个任务(任务不可见),参与者选一个数字(即“蟹脚”)划去,已划去的数字不能再划,所有人划完后任务公开,每个人执行所划数字对应的任务.小丽随机划去一个数字,则她执行“扫地”任务的概率是( )
C、12
D、6
6. 有一种纸上游戏叫“划蟹脚”,如图,每个数字连线着一个任务(任务不可见),参与者选一个数字(即“蟹脚”)划去,已划去的数字不能再划,所有人划完后任务公开,每个人执行所划数字对应的任务.小丽随机划去一个数字,则她执行“扫地”任务的概率是( )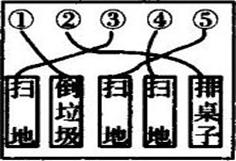 A、
A、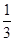 B、
C、
D、1
7. AB为半圆O的直径,现将一块等腰直角三角板如图放置,锐角顶点P在半圆上。斜边过点B.一条直角边交该半圆于点Q.若AB=2,则线段BQ的长为( )
B、
C、
D、1
7. AB为半圆O的直径,现将一块等腰直角三角板如图放置,锐角顶点P在半圆上。斜边过点B.一条直角边交该半圆于点Q.若AB=2,则线段BQ的长为( ) A、 B、 C、 D、8. 如图,矩形ABCD中,AB=9,BC=6,点E.F分别是边BC,CD上的点.且AE⊥EF,则AF的最小值是( )
A、 B、 C、 D、8. 如图,矩形ABCD中,AB=9,BC=6,点E.F分别是边BC,CD上的点.且AE⊥EF,则AF的最小值是( ) A、10 B、 C、
A、10 B、 C、 D、9
9. 定义:如果抛物线:y=a1x2+bx+c1(a1≠0)与抛物线y=a2x2+bx+c2(a2≠0)满足:a1+a2=0,c1+c2=0,则称这两条抛物线互为“同胞抛物线”.现有下列结论:①抛物线y=(x+1)2-2的同胞抛物线是抛物线y=(x+1)2+2;②若两条抛物线互为同胞抛物线,则它们的顶点关于原点对称;③已知抛物线C1与抛物线C2互为同胞抛物线,若点M(2,3)在抛物线C1上,则N(-3,-2)在抛物线C2上;④已知抛物线C1与抛物线C2互为同胞抛物线。则它们一定有两个不同的交点.
D、9
9. 定义:如果抛物线:y=a1x2+bx+c1(a1≠0)与抛物线y=a2x2+bx+c2(a2≠0)满足:a1+a2=0,c1+c2=0,则称这两条抛物线互为“同胞抛物线”.现有下列结论:①抛物线y=(x+1)2-2的同胞抛物线是抛物线y=(x+1)2+2;②若两条抛物线互为同胞抛物线,则它们的顶点关于原点对称;③已知抛物线C1与抛物线C2互为同胞抛物线,若点M(2,3)在抛物线C1上,则N(-3,-2)在抛物线C2上;④已知抛物线C1与抛物线C2互为同胞抛物线。则它们一定有两个不同的交点.其中正确的个数是( )
A、1 B、2 C、3 D、410. 如图·在Rt△ABC中,∠C=90°,AC=6,BC=8.在△ABC内放入边长为1的正方形纸片,每两张纸片都不重叠,则最多能放入的正方形纸片的张数是( ) A、15 B、16 C、17 D、18
A、15 B、16 C、17 D、18二、填空.
-
11. 已知两个相似三角形的对应边之比为2,则它们的周长之比是 .12. 已知关于x的二次函数y=3x2+2x+m+1的图象经过点(1,6),则m的值为.
13. 甲、乙两人玩。锤子、剪刀、布”的游戏.
若两人同时随机出一个手势,则甲获胜的概率为 .
14. 如图,已知点G为△ABc的重心,过点G作DE∥BC。交AB于点D,交AC于点E,若BC=15,则线段DE的长为 . 15. 如图.正五边形硬纸片ABCDE在桌面上沿直线l无滑动地翻滚一周,若正五边形ABCDE的外接圈的半径长为3cm,则正五边形的中心O运动的路径长为cm
15. 如图.正五边形硬纸片ABCDE在桌面上沿直线l无滑动地翻滚一周,若正五边形ABCDE的外接圈的半径长为3cm,则正五边形的中心O运动的路径长为cm 16. 如图,在平面直角坐标系xOy中,已知抛物线 与x轴相交于A,B两点,过点B的直线 与抛物线相交于点C.将直线BC沿y轴向下平移4个单位后,与x轴,y轴分别相交于D,E两点.点F,G分别为抛物线的对称轴和直线DE上的动点.则CF+FG的最小值为 .
16. 如图,在平面直角坐标系xOy中,已知抛物线 与x轴相交于A,B两点,过点B的直线 与抛物线相交于点C.将直线BC沿y轴向下平移4个单位后,与x轴,y轴分别相交于D,E两点.点F,G分别为抛物线的对称轴和直线DE上的动点.则CF+FG的最小值为 .
三、解答题
-
17. 根据下列条件,求 的值(1)、(2)、18. 如图,已知抛物线 的顶点坐标为(2,-1),与x轴交于A,B两点(点A在点B的左边).与y轴交于点C,一次函数y=kx+c经过点B和点C.
 (1)、求点B的坐标·(2)、根据图象,直接写出不等式kx+c≤x2+bx+c的解集.19. 如图,AB是圆O的直径,弦AC=2,∠ABC=30°.
(1)、求点B的坐标·(2)、根据图象,直接写出不等式kx+c≤x2+bx+c的解集.19. 如图,AB是圆O的直径,弦AC=2,∠ABC=30°.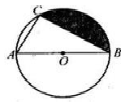 (1)、求证:(2)、求图中阴影部分的面积.20. 羽毛球团体赛小组赛比赛规则:两队之间进行五局比赛,其中三局单打.两局双打,五局比赛必须全部打完,赢得三局及以上的队获胜.假如甲、乙两队每局获胜的机会相同.(1)、若前四局双方战成2:2,那么甲队最终获胜的概率是多少?(2)、现甲队在前两局比赛中已取得2:0的领先,那么甲队最终获胜的概率是多少?(用“列表”或“画树状图”给出分析过程)21. 如图.已知等腰Rt△ABC,∠ABC=90°,AB=6,点D是BA延长线上的一点,过点C作CE⊥AC.交△BCD的外接圆于点E,连结BE,CD·
(1)、求证:(2)、求图中阴影部分的面积.20. 羽毛球团体赛小组赛比赛规则:两队之间进行五局比赛,其中三局单打.两局双打,五局比赛必须全部打完,赢得三局及以上的队获胜.假如甲、乙两队每局获胜的机会相同.(1)、若前四局双方战成2:2,那么甲队最终获胜的概率是多少?(2)、现甲队在前两局比赛中已取得2:0的领先,那么甲队最终获胜的概率是多少?(用“列表”或“画树状图”给出分析过程)21. 如图.已知等腰Rt△ABC,∠ABC=90°,AB=6,点D是BA延长线上的一点,过点C作CE⊥AC.交△BCD的外接圆于点E,连结BE,CD· (1)、求证;△ADC∽△CEB;(2)、若CE= ,求△BCD外接圆的半径长.22. 某网店销售一种产品。这种产品的成本价为10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/件.市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.
(1)、求证;△ADC∽△CEB;(2)、若CE= ,求△BCD外接圆的半径长.22. 某网店销售一种产品。这种产品的成本价为10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/件.市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示. (1)、当12≤x≤18时。求y与x之间的函数关系式;(2)、求每天的销售利润w(元)与销售价x(元/件)之间的函数关系式.并求出每件销售价为多少元时.每天的销售利润最大?最大利润是多少?23. 如图1,已知Rt△ABC和Rt△DEF.点C与点E重合,点A,C(E),D在同一条直线上,且∠ACB=∠EDF=90°,AC=BC=20,DE=20,DF=15.如图2,△DEF从图1的位置出发.以每秒4个单位的速度沿CA佝△ABC运动,同时,点P从点B出发,以每秒2 个单位沿BA向点A运动,当点E与点A重合时。△DEF与点P都停止运动,EF与BC交于点Q,连接PQ,PE,设移动时间为t秒。
(1)、当12≤x≤18时。求y与x之间的函数关系式;(2)、求每天的销售利润w(元)与销售价x(元/件)之间的函数关系式.并求出每件销售价为多少元时.每天的销售利润最大?最大利润是多少?23. 如图1,已知Rt△ABC和Rt△DEF.点C与点E重合,点A,C(E),D在同一条直线上,且∠ACB=∠EDF=90°,AC=BC=20,DE=20,DF=15.如图2,△DEF从图1的位置出发.以每秒4个单位的速度沿CA佝△ABC运动,同时,点P从点B出发,以每秒2 个单位沿BA向点A运动,当点E与点A重合时。△DEF与点P都停止运动,EF与BC交于点Q,连接PQ,PE,设移动时间为t秒。 (1)、求BP和BQ;(用含t的代数式表示)(2)、当△BPQ为直角三角形时,求t的值;(3)、四边形BPEQ的面积能否达到100?若能,请求出此时t的值;若不能,请说明理由·24. 如图,在平面直角坐标系xOy中,直线 与抛物线 (b,c为常数)交于点A(-1,0)和B(3,3),点C是直线 下方抛物线上的一个动点·
(1)、求BP和BQ;(用含t的代数式表示)(2)、当△BPQ为直角三角形时,求t的值;(3)、四边形BPEQ的面积能否达到100?若能,请求出此时t的值;若不能,请说明理由·24. 如图,在平面直角坐标系xOy中,直线 与抛物线 (b,c为常数)交于点A(-1,0)和B(3,3),点C是直线 下方抛物线上的一个动点· (1)、求抛物线的函数解析式;(2)、过点C作CD⊥AB,垂足为点D。当线段CD的长度最大时,求点C的坐标;(3)、在(2)的条件下,点M是x轴正半轴上一点,过点M作x轴的垂线,交抛物线于点N.是否这样的点M,使得以点A,M,N为顶点的三角形与△ABC相似?若存在,请直接写出所有符合条件的点M的坐标,若不存在。请说明理由.
(1)、求抛物线的函数解析式;(2)、过点C作CD⊥AB,垂足为点D。当线段CD的长度最大时,求点C的坐标;(3)、在(2)的条件下,点M是x轴正半轴上一点,过点M作x轴的垂线,交抛物线于点N.是否这样的点M,使得以点A,M,N为顶点的三角形与△ABC相似?若存在,请直接写出所有符合条件的点M的坐标,若不存在。请说明理由.