黑龙江省牡丹江市2018年中考数学试卷

试卷更新日期：2019-01-05 类型：中考真卷

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的有（）个．

A、0 B、1 C、2 D、3

查看试题解析
2. 下列运算正确的是（）

A、2a^﹣³•a⁴=2a^﹣¹² B、（﹣3a²）³=﹣9a⁶ C、 a²÷a× =a² D、a•a³+a²•a²=2a⁴

查看试题解析
3. 由5个完全相同的小长方体搭成的几何体的主视图和左视图如图所示，则这个几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
4. 在函数y= $\sqrt{x + 3}$ 中，自变量x的取值范围是（）

A、x≤﹣3 B、x≥﹣3 C、x＜﹣3 D、x＞﹣3

查看试题解析
5. 一组数据4，2，x，3，9的平均数为4，则这组数据的众数和中位数分别是（）

A、3，2 B、2，2 C、2，3 D、2，4

查看试题解析
6. 如图，在长为15，宽为12的矩形中，有形状、大小完全相同的5个小矩形，则图中阴影部分的面积为（）

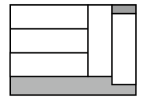A、35 B、45 C、55 D、65

查看试题解析
7. 如图，△ABC内接于⊙O，若sin∠BAC= $\frac{1}{3}$ ，BC=2 $\sqrt{6}$ ，则⊙O的半径为（）

A、 3 B、 6 C、 4 D、 2

查看试题解析
8. 如图，△ABC三个顶点的坐标分别是A（1，﹣1），B（2，﹣2），C（4，﹣1），将△ABC绕着原点O旋转75°，得到△A₁B₁C₁ ，则点B₁的坐标为（）

A、（，）或（﹣ ，﹣ ） B、（，）或（﹣ ，﹣ ） C、（﹣ ，﹣ ）或（，） D、（﹣ ，﹣ ）或（，）

查看试题解析
9. 将抛物线y=x²+2x+3向下平移3个单位长度后，所得到的抛物线与直线y=3的交点坐标是（）

A、（0，3）或（﹣2，3） B、（﹣3，0）或（1，0） C、（3，3）或（﹣1，3） D、（﹣3，3）或（1，3）

查看试题解析
10. 如图，E为矩形ABCD的边AB上一点，将矩形沿CE折叠，使点B恰好落在ED上的点F处，若BE=1，BC=3，则CD的长为（）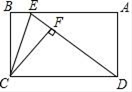

A、6 B、5 C、4 D、3

查看试题解析
11. 如图，正方形ABCD中，E为CD的中点，AE的垂直平分线分别交AD，BC及AB的延长线于点F，G，H，连接HE，HC，OD，连接CO并延长交AD于点M．则下列结论中：
①FG=2AO；②OD∥HE；③ $\frac{B H}{E C} = \frac{A M}{M D}$ ；④2OE²=AH•DE；⑤GO+BH=HC

正确结论的个数有（）

A、2 B、3 C、4 D、5

查看试题解析
12. 如图，直线y=kx﹣3（k≠0）与坐标轴分别交于点C，B，与双曲线y=﹣ $\frac{2}{x}$ （x＜0）交于点A（m，1），则AB的长是（）

A、 2 B、 C、 2 D、

查看试题解析

二、填空题

13. 从党的“十八大”到“十九大”经历43800小时，我国的“天宫、蛟龙、天眼、悟空、墨子、大飞机”等各项科技创新成果“井喷”式发展，这些记录下了党的极不平凡的壮阔进程，请将数43800用科学记数法表示为

查看试题解析
14. 如图，AC=BC，请你添加一对边或一对角相等的条件，使AD=BE．你所添加的条件是．

查看试题解析
15. 同时抛掷两枚质地均匀的硬币，一枚硬币正面向上，一枚硬币反面向上的概率是．

查看试题解析
16. 一列数1，4，7，10，13，……按此规律排列，第n个数是

查看试题解析
17. 小明按标价的八折购买了一双鞋，比按标价购买节省了40元，这双鞋的实际售价为元．

查看试题解析
18. 用一个圆心角为240°，半径为3的扇形作一个圆锥的侧面，这个圆锥的底面圆的半径为．

查看试题解析
19. 矩形ABCD中，AB=6，AD=8，点M在对角线AC上，且AM：MC=2：3，过点M作EF⊥AC交AD于点E，交BC于点F．在AC上取一点P，使∠MEP=∠EAC，则AP的长为．

查看试题解析
20. 如图，抛物线y=ax²+bx+c（a≠0）的对称轴为直线x=﹣1，下列结论中：
①abc＜0；②9a﹣3b+c＜0；③b²﹣4ac＞0；④a＞b，

正确的结论是（只填序号）

查看试题解析

三、解答题

21. 先化简，再求值： $\frac{x^{2} - 1}{x^{2} - 2 x + 1} \cdot \frac{1}{x + 1} - \frac{1}{x}$ ，其中x=2．

查看试题解析
22. 如图，在⊙O中 $\overset{⌢}{A B} = 2 \overset{⌢}{A C}$ ，AD⊥OC于D．求证：AB=2AD．

查看试题解析
23. 在四边形ABCD中，∠B=∠C=90°，AB=3，BC=4，CD=1．以AD为腰作等腰△ADE，使∠ADE=90°，过点E作EF⊥DC交直线CD于点F．请画出图形，并直接写出AF的长．

查看试题解析
24. 如图，抛物线y=﹣x²+bx+c经过A（﹣1，0），B（3，0）两点，交y轴于点C，点D为抛物线的顶点，连接BD，点H为BD的中点．请解答下列问题：
（注：抛物线y=ax²+bx+c（a≠0）的对称轴是直线x=﹣ $\frac{b}{2 a}$ ，顶点坐标为（﹣ $\frac{b}{2 a}$ ， $\frac{4 a c - b^{2}}{4 a}$ ）

(1)、求抛物线的解析式及顶点D的坐标；

(2)、在y轴上找一点P，使PD+PH的值最小，则PD+PH的最小值为．

查看试题解析
25. 某校在一次社会实践活动中，组织学生参观了虎园、烈士陵园、博物馆和植物园，为了解本次社会实践活动的效果，学校随机抽取了部分学生，对“最喜欢的景点”进行了问卷调查，并根据统计结果绘制了如下不完整的统计图．其中最喜欢烈士陵园的学生人数与最喜欢博物馆的学生人数之比为2：1，请结合统计图解答下列问题：

(1)、本次活动抽查了名学生；

(2)、请补全条形统计图；

(3)、在扇形统计图中，最喜欢植物园的学生人数所对应扇形的圆心角是度；

(4)、该校此次参加社会实践活动的学生有720人，请求出最喜欢烈士陵园的人数约有多少人？

查看试题解析
26. 在一条笔直的公路上依次有A，C，B三地，甲、乙两人同时出发，甲从A地骑自行车去B地，途经C地休息1分钟，继续按原速骑行至B地，甲到达B地后，立即按原路原速返回A地；乙步行从B地前往A地．甲、乙两人距A地的路程y（米）与时间x（分）之间的函数关系如图所示，请结合图象解答下列问题：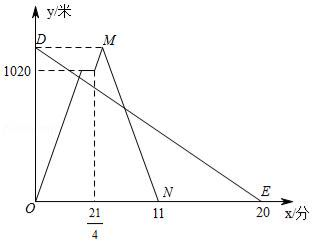

(1)、请写出甲的骑行速度为米/分，点M的坐标为；

(2)、求甲返回时距A地的路程y与时间x之间的函数关系式（不需要写出自变量的取值范围）；

(3)、请直接写出两人出发后，在甲返回A地之前，经过多长时间两人距C地的路程相等．

查看试题解析
27. 在等腰△ABC中，∠B=90°，AM是△ABC的角平分线，过点M作MN⊥AC于点N，∠EMF=135°．将∠EMF绕点M旋转，使∠EMF的两边交直线AB于点E，交直线AC于点F，请解答下列问题：

(1)、当∠EMF绕点M旋转到如图①的位置时，求证：BE+CF=BM；

(2)、当∠EMF绕点M旋转到如图②，图③的位置时，请分别写出线段BE，CF，BM之间的数量关系，不需要证明；

(3)、在（1）和（2）的条件下，tan∠BEM= $\sqrt{3}$ ，AN= $\sqrt{2}$ +1，则BM= ， CF= ．

查看试题解析
28. 某书店现有资金7700元，计划全部用于购进甲、乙、丙三种图书共20套，其中甲种图书每套500元，乙种图书每套400元，丙种图书每套250元．书店将甲、乙、丙三种图书的售价分别定为每套550元，430元，310元．设书店购进甲种图书x套，乙种图书y套，请解答下列问题：

(1)、请求出y与x的函数关系式（不需要写出自变量的取值范围）；

(2)、若书店购进甲、乙两种图书均不少于1套，则该书店有几种进货方案？

(3)、在（1）和（2）的条件下，根据市场调查，书店决定将三种图书的售价作如下调整：甲种图书的售价不变，乙种图书的售价上调a（a为正整数）元，丙种图书的售价下调a元，这样三种图书全部售出后，所获得的利润比（2）中某方案的利润多出20元，请直接写出书店是按哪种方案进的货及a的值．

查看试题解析
29. 菱形ABCD在平面直角坐标系中的位置如图所示，对角线AC与BD的交点E恰好在y轴上，过点D和BC的中点H的直线交AC于点F，线段DE，CD的长是方程x²﹣9x+18=0的两根，请解答下列问题：

(1)、求点D的坐标；

(2)、若反比例函数y= $\frac{k}{x}$ （k≠0）的图象经过点H，则k=；

(3)、点Q在直线BD上，在直线DH上是否存在点P，使以点F，C，P，Q为顶点的四边形是平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析