河南省驻马店市确山县2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期:2019-01-05 类型:期末考试
一、单选题
-
1. 下列作品中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 雾霾天气是一种大气污染状态,造成这种天气的“元凶”是PM2.5,PM2.5是指直径小于或等于0.0000025米的可吸入肺的微小颗粒,将数据0.0000025科学记数法表示为( )A、2.5×106 B、2.5×10﹣6 C、0.25×10﹣6 D、0.25×1073. 下列根式是最简二次根式的是( )A、
2. 雾霾天气是一种大气污染状态,造成这种天气的“元凶”是PM2.5,PM2.5是指直径小于或等于0.0000025米的可吸入肺的微小颗粒,将数据0.0000025科学记数法表示为( )A、2.5×106 B、2.5×10﹣6 C、0.25×10﹣6 D、0.25×1073. 下列根式是最简二次根式的是( )A、 B、
B、 C、
D、
C、
D、 4. 下列计算正确的是( )A、
4. 下列计算正确的是( )A、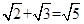 B、a3•a2=a6
C、a7÷a=a6
D、(﹣2a2)3=86
5. 解分式方程 时,去分母后变形为( )A、
B、a3•a2=a6
C、a7÷a=a6
D、(﹣2a2)3=86
5. 解分式方程 时,去分母后变形为( )A、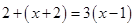 B、
B、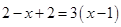 C、
C、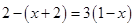 D、
D、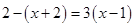 6. 如图,△ABC和△DEF中,AB=DE、∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( )
6. 如图,△ABC和△DEF中,AB=DE、∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( )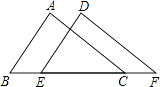 A、AC∥DF B、∠A=∠D C、AC=DF D、∠ACB=∠F7. 如图,OC平分∠AOB,点P是射线OC上的一点,PD⊥OB于点D,且PD=3,动点Q在射线OA上运动,则线段PQ的长度不可能是( )
A、AC∥DF B、∠A=∠D C、AC=DF D、∠ACB=∠F7. 如图,OC平分∠AOB,点P是射线OC上的一点,PD⊥OB于点D,且PD=3,动点Q在射线OA上运动,则线段PQ的长度不可能是( ) A、2 B、3 C、4 D、58. 长和宽分别为a,b的长方形的周长为14,面积为10,则a2b+ab2的值为( )A、24 B、35 C、70 D、1409. 一项工程,一半由甲单独做需要m小时完成,另一半由乙单独做需要n小时完成,则甲、乙合做这项工程所需的时间为( )A、
A、2 B、3 C、4 D、58. 长和宽分别为a,b的长方形的周长为14,面积为10,则a2b+ab2的值为( )A、24 B、35 C、70 D、1409. 一项工程,一半由甲单独做需要m小时完成,另一半由乙单独做需要n小时完成,则甲、乙合做这项工程所需的时间为( )A、 小时
B、
小时
B、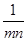 小时
C、
小时
C、 小时
D、
小时
D、 小时
10. 如图,在△ABC中,AB=AC,AD、CE是△ABC的两条中线,P是AD上一个动点,则下列线段的长度等于BP+EP最小值的是( )
小时
10. 如图,在△ABC中,AB=AC,AD、CE是△ABC的两条中线,P是AD上一个动点,则下列线段的长度等于BP+EP最小值的是( )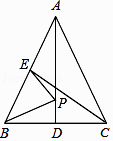 A、BC B、CE C、AD D、AC
A、BC B、CE C、AD D、AC二、填空题
-
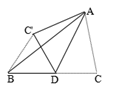
11. 计算:(1﹣ )0﹣(﹣ )﹣2= .12. 若代数式 有意义,则x的取值范围为 .13. 若 是关于x的完全平方式,则m= .14. 已知等腰三角形的两边长分别为5 和2 ,则这个等腰三角形的周长为 .15. 如图,AD是△ABC的中线,且∠ADC=60°,BC=4,把△ADC沿直线AD折叠后,点C落在点C'的位置上.则B C'=.
三、解答题
-
16.(1)、分解因式:a2(x﹣y)+4b2(y﹣x)(2)、计算:17. 先化简,再求值(1)、(2x+y)2+(x﹣y)(x+y)﹣5x(x﹣y),其中x= +1,y=1﹣(2)、 ÷(1﹣ ),其中x= ﹣118. 如图,在△ABC中,∠A>∠B.
 (1)、作边AB的垂直平分线DE,与AB,BC分别相交于点D,E(用尺规作图,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,连接AE,若∠B=50°,求∠AEC的度数.19. 长春外国语学校为了创建全省“最美书屋”,购买了一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多5元.已知学校用12000元购买的科普类图书的本数与用9000元购买的文学类图书的本数相等,求学校购买的科普类图书和文学类图书平均每本的价格各是多少元?20. 如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)、作边AB的垂直平分线DE,与AB,BC分别相交于点D,E(用尺规作图,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,连接AE,若∠B=50°,求∠AEC的度数.19. 长春外国语学校为了创建全省“最美书屋”,购买了一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多5元.已知学校用12000元购买的科普类图书的本数与用9000元购买的文学类图书的本数相等,求学校购买的科普类图书和文学类图书平均每本的价格各是多少元?20. 如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD. (1)、求证:△ABC≌△AED;(2)、当∠B=140°时,求∠BAE的度数.21. 探究应用:(1)、计算:①(x+2)(x2﹣2x+4);②(2m+n)(4m2﹣2mn+n2);(2)、上面的整式乘法计算结果比较简洁,类比学习过的平方差公式,完全平方公式的推导过程,通过观察,写出你又发现了一个新的乘法公式(请用含a、b的字母表示)(3)、下列各式能用你(2)中发现的乘法公式计算的是哪个式子(只填字母代号)
(1)、求证:△ABC≌△AED;(2)、当∠B=140°时,求∠BAE的度数.21. 探究应用:(1)、计算:①(x+2)(x2﹣2x+4);②(2m+n)(4m2﹣2mn+n2);(2)、上面的整式乘法计算结果比较简洁,类比学习过的平方差公式,完全平方公式的推导过程,通过观察,写出你又发现了一个新的乘法公式(请用含a、b的字母表示)(3)、下列各式能用你(2)中发现的乘法公式计算的是哪个式子(只填字母代号)A(x+1)(x2+x+1) B.(3a+b)(3a2﹣3ab+b2)
C(m+2n)(m2﹣2mn+4n2) D(5+a)(25+10a+a2)
(4)、直接用你发现的公式计算:(2a+3b)(4a2﹣6ab+9b2).22. “魅力数学”社团活动时,张老师出示了如下问题:如图①,已知四边形ABCD中,AC平分∠DAB,∠DAB=120°,∠B与∠D互补,试探究线段AB,AD,AC之间的数量关系;
小敏反复探索,不得其解,张老师提示道:“数学中常通过把一个问题特殊化来找到解题思路”,于是,小敏想,若将四边形ABCD特殊化,看如何解决问题:
 (1)、特殊情况入手
(1)、特殊情况入手添加条件:“∠B=∠D”,如图②易知在Rt△CDA中,∠DCA=30°,所以,写出边AD与AC之间的数量关系,同理可得AB与AC的数量关系,由此得AB,AD,AC之间的数量关系;
(2)、解决原来问题受到(1)的启发,在原问题上,添加辅助线,过点C分别作AB,AD的垂线,垂足分别为E、F,如图③,请写出探究过程;
(3)、解后反思“一题多解”是数学解题的魅力之一,小敏在张老师的引导下,受探究结论的启发,结合图中的60°角,通过构造等边三角形,利用三角形全等同样解决了该问题,请在图①中作出辅助线,并简述你的探究过程.