河南省周口市西华县2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期:2019-01-05 类型:期末考试
一、单选题
-
1. 分式 可变形为( )A、
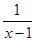 B、
B、 C、
C、 D、
D、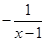 2. 下列图形中,不是轴对称图形的是( )A、
2. 下列图形中,不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 若一个三角形两边长分别是3、7,则第三边长可能是( )A、4 B、8 C、10 D、114. 计算正确的是( )A、
3. 若一个三角形两边长分别是3、7,则第三边长可能是( )A、4 B、8 C、10 D、114. 计算正确的是( )A、 B、
B、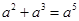 C、
C、 D、
D、 5. 有意义的条件是( )A、
5. 有意义的条件是( )A、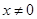 B、
B、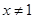 C、
C、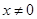 且
且 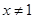 D、
D、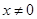 或
或 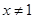 6. 点A(a + 1,a)关于x轴对称的点在第一象限,则a的取值范围是( )A、-1< a < 0 B、 C、 D、a<-17. 下列各式变式正确的个数是( )
6. 点A(a + 1,a)关于x轴对称的点在第一象限,则a的取值范围是( )A、-1< a < 0 B、 C、 D、a<-17. 下列各式变式正确的个数是( )①( )(b-a)=b2-a2②( )( ) ③(a+b)2=(a-b)2+4ab④(a+b)2+(a-b)2=2a2+2b2
A、1 B、2 C、3 D、48. 如图,直线l外有不重合的两点A,B.在直线l上求一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B'.②连接AB'交直线l于点C,则点C即为所求.在解决这个问题时,没有用到的知识点是( ) A、线段的垂直平分线性质 B、两点之间线段最短 C、三角形两边之和大于第三边 D、角平分线的性质9. 观察下列图形,则第n个图形中三角形的个数是( )
A、线段的垂直平分线性质 B、两点之间线段最短 C、三角形两边之和大于第三边 D、角平分线的性质9. 观察下列图形,则第n个图形中三角形的个数是( ) A、2n-1 B、
A、2n-1 B、 C、4n+1
D、4n-1
10. 如图,△ABC是等边三角形,AD是角平分线,△ADE也是等边三角形,下列结论:①AD
C、4n+1
D、4n-1
10. 如图,△ABC是等边三角形,AD是角平分线,△ADE也是等边三角形,下列结论:①AD BC.②EF
BC.②EF  FD.③BE
FD.③BE  BD.④AC
BD.④AC  AE.其中正确的个数是( )
AE.其中正确的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 计算: .12. 分式 的值为0,则 .13. 如图,△ABC中,AB AC,AB的垂直平分线DE交AC于D,交AB于E,且BD平分∠ABC,则∠BDC=度.
 14. 观察下列各式的规律:
14. 观察下列各式的规律:……
可得到 .
15. 如图,在△ABC中,点P、Q分别是BC、AC边上的点,PS AC,PR AB,若AQ PQ,PR PS,则下列结论:①AS AR;②QP∥AR;③△BRP ≌△CPS;④S四边形ARPQ= .其中正确的结论有(填序号).
三、解答题
-
16. 分解因式:① -a4+16;②6xy2-9x2y-y317. 已知4x=3y,求代数式(x-2y)2-(x-y)(x+y)-2y2的值.18. AD,AE分别是△ABC的高和角平分线.
 (1)、已知∠B=30°,∠C=60°,求∠DAE的度数;(2)、设∠B= x,∠C= y(x < y),请直接写出∠DAE的度数 . (用含x ,y的代数式表示)19. ABN和△ACM的位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)、已知∠B=30°,∠C=60°,求∠DAE的度数;(2)、设∠B= x,∠C= y(x < y),请直接写出∠DAE的度数 . (用含x ,y的代数式表示)19. ABN和△ACM的位置如图所示,AB=AC,AD=AE,∠1=∠2.
求证:
(1)、BD=CE;(2)、∠M=∠N.20. 化简: ,然后在不等式x≤2的非负整数解中选择一个适当的数代入求值.21. 家庭号超市用5000元购进一批新品种的苹果进行试销,由于销售状况良好,超市又调拨11000元资金购进该品种苹果,但这次的进货价比试销时每千克多了0.5元,购进苹果数量是试销时的2倍.(1)、试销时该品种苹果的进货价是每千克多少元?(2)、如果超市将该品种苹果按每千克7元的定价出售,当大部分苹果售出后,余下的400千克按定价的七折(“七折”即定价的70%)售完,那么超市在这两次苹果销售中共盈利多少元?22. 如图,已知△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1 cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),
则:
(1)、BP = cm,BQ = cm.(用含t的代数式表示)(2)、当t为何值时,△PBQ是直角三角形?23. 如图(1),在四边形ABCD中,已知∠ABC ∠ADC 180°,AB AD,AB AD,点E在CD的延长线上,∠1 ∠2.
∠ADC 180°,AB AD,AB AD,点E在CD的延长线上,∠1 ∠2.  (1)、求证:∠3 ∠E;(2)、求证:CA平分∠BCD;(3)、如图(2),设AF是△ABC的边BC上的高,求证:CE 2AF.
(1)、求证:∠3 ∠E;(2)、求证:CA平分∠BCD;(3)、如图(2),设AF是△ABC的边BC上的高,求证:CE 2AF.