河南省信阳市浉河区2017-2018学年八年级上学期数学期末考试试卷

试卷更新日期：2019-01-05 类型：期末考试

进入出卷网下载

一、单选题

1. 剪纸是我国传统的民间艺术，下列剪纸作品中，是轴对称图形的为（　　）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、3a+2b=5ab B、5a﹣2a=3a C、b²•b³=b⁶ D、（x+y）²=x²+y²

查看试题解析
3. 已知一个等腰三角形两边长分别为3，7，那么它的周长是（）

A、17 B、13 C、13或17 D、10或13

查看试题解析
4. 如图，AB∥CD，BC∥AD，AB=CD，BE=DF，图中全等的三角形的对数是（）

A、3 B、4 C、5 D、6

查看试题解析
5. 若分式 $\frac{x^{2} - 9}{x - 3}$ 的值为0，则x的值等于（）

A、0 B、±3 C、3 D、﹣3

查看试题解析
6. 如图，DE是△ABC中AC边的垂直平分线，若BC=8，AB=10，则△EBC的周长是（）

A、13 B、16 C、18 D、20

查看试题解析
7. 已知a^m=2，aⁿ=3，则a^n+m=（）

A、2 B、3 C、5 D、6

查看试题解析
8. 一个正六边形和两个等边三角形的位置如图所示，∠3=70°，则∠1+∠2=（）

A、40° B、50° C、60° D、70°

查看试题解析
9. 下列计算结果正确的有（）
① $\frac{3 x}{x^{2}}$ • $\frac{x}{3 x}$ = $\frac{1}{x}$ ；②8a²b²•（﹣ $\frac{3 a}{4 b^{2}}$ ）=﹣6a³；③ $\frac{a}{a^{2} - 1}$ ÷ $\frac{a^{2}}{a^{2} + a}$ = $\frac{1}{a - 1}$ ； ④a÷b• $\frac{1}{b}$ =a．

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 当x分别取﹣2015、﹣2014、﹣2013、…，、﹣2、﹣1、0、1、 $\frac{1}{2}$ 、 $\frac{1}{3}$ 、…、 $\frac{1}{2013}$ 、 $\frac{1}{2014}$ 、 $\frac{1}{2015}$ 时，计算分式 $\frac{x^{2} - 1}{x^{2} + 1}$ 的值，再将所得结果相加，其和等于（）

A、﹣1 B、1 C、0 D、2015

查看试题解析

二、填空题

11. 如图，∠ABD=76°，∠C=38°，BC=30cm，则BD的长为．

查看试题解析
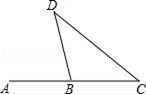12. 如图，在△ABC中，AB=AC，∠A=40°，AB的垂直平分线交AB于点D，交AC于点E，连接BE，则∠CBE的度数为．

查看试题解析
13. 若x²+mx+9是一个完全平方式，则m的值是．

查看试题解析
14. 如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S_△ABC=8cm² ，则图中阴影部分的面积等于cm²

查看试题解析
15. 如图，在△ABC中，AB=AC=24厘米，BC=16厘米，点D为AB的中点，点P在线段BC上以4厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．当点Q的运动速度为厘米/秒时，能够在某一时刻使△BPD与△CQP全等．

查看试题解析

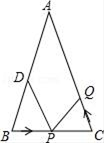
三、解答题

16. 先化简（ $\frac{a^{2}}{a - 2} - \frac{1}{a - 2}$ ）÷ $\frac{a^{2} - 2 a + 1}{a - 2}$ ，然后从1、2、3中选取一个你认为合适的数作为a的值代入求值．

查看试题解析
17. 如图，在平面直角坐标系中，△ABC的三个顶点分别为A（2，3），B（3，1），C（-2，-2）.

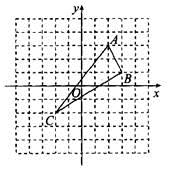(1)、请在图中作出△ABC关于y轴的轴对称图形△A′B′C′（A，B，C的对称点分别是A′，B′，C′），并直接写出A′，B′，C′的坐标.

(2)、求△A′B′C′的面积.

查看试题解析
18. 按要求完成计算：

(1)、先化简，再求值：（4ab³﹣8a²b²）÷4ab+（2a+b）（2a﹣b），其中a=2，b=1．

(2)、因式分解：3x²﹣6axy+3ay² ．

查看试题解析
19. 用尺规作图（不写作法、保留作图痕迹，标注结果）

(1)、作线段AB（如图1所示）的中垂线EF．

(2)、作∠AOB（如图2所示）的角平分线OC．

查看试题解析
20. 列方程或方程组解应用题：
为响应市政府“绿色出行”的号召，小张上班由自驾车改为骑公共自行车．已知小张家距上班地点10千米．他用骑公共自行车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程少45千米，他从家出发到上班地点，骑公共自行车方式所用的时间是自驾车方式所用的时间的4倍．小张用骑公共自行车方式上班平均每小时行驶多少千米？

查看试题解析
21. 如图，∠ACB=90°，AC=BC，BE⊥CE于E，AD⊥CE于D，BE=3cm，AD=9cm．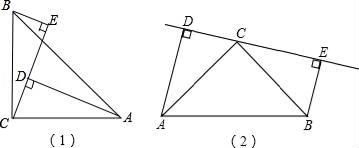

求：

(1)、DE的长；

(2)、若CE在△ABC的外部（如图），其它条件不变，DE的长是多少？

查看试题解析
22. 阅读下面材料：
学习了三角形全等的判定方法（即“SAS”“ASA”“AAS”“SSS”）和直角三角形全等的判定方法（即“HL”）后，小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究

小聪将命题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E．

小聪的探究方法是对∠B分为“直角、钝角、锐角”三种情况进行探究．

第一种情况：当∠B 是直角时，如图1，△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E=90°，根据“HL”定理，可以知道Rt△ABC≌Rt△DEF．

第二种情况：当∠B 是锐角时，如图2，BC=EF，∠B=∠E＜90°，在射线EM上有点D，使DF=AC，画出符合条件的点D，则△ABC和△DEF的关系是；

A．全等 B．不全等 C．不一定全等

第三种情况：当∠B是钝角时，如图3，在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E＞90°．过点C作AB边的垂线交AB延长线于点M；同理过点F作DE边的垂线交DE延长线于N，根据“ASA”，可以知道△CBM≌△FEN，请补全图形，进而证出△ABC≌△DEF．

查看试题解析
23. 在Rt△ABC中，BC=AC，∠ACB=90°，点D为射线AB上一点，连接CD，过点C作线段CD的垂线l，在直线l上，分别在点C的两侧截取与线段CD相等的线段CE和CF，连接AE、BF．

(1)、当点D在线段AB上时（点D不与点A、B重合），如图1
①请你将图形补充完整；

②线段BF、AD所在直线的位置关系为，线段BF、AD的数量关系为；

(2)、当点D在线段AB的延长线上时，如图2
①请你将图形补充完整；

②在（1）中②问的结论是否仍然成立？如果成立请进行证明，如果不成立，请说明理由．

查看试题解析