河南省新乡市卫辉市2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期:2019-01-05 类型:期末考试
一、单选题
-
1. 下列各数中最小的是( )A、
 B、
C、-
D、0
2. 如图,数轴上表示1、 的对应点分别为点A,点B.若点A是BC的中点,则点C所表示的数为 ( )
B、
C、-
D、0
2. 如图,数轴上表示1、 的对应点分别为点A,点B.若点A是BC的中点,则点C所表示的数为 ( )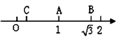 A、
A、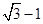 B、
B、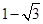 C、
C、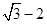 D、
D、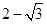 3. 若直角三角形的三边a、b、c满足a2-4a+4+ =0,则第三边c的长度是( )A、 B、 C、 或 D、5或134. 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
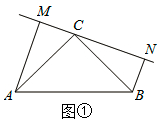
3. 若直角三角形的三边a、b、c满足a2-4a+4+ =0,则第三边c的长度是( )A、 B、 C、 或 D、5或134. 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )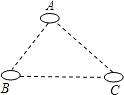 A、在AC,BC两边高线的交点处 B、在AC,BC两边中线的交点处 C、在AC,BC两边垂直平分线的交点处 D、在∠A,∠B两内角平分线的交点处5. 已知一个样本容量为50,在频数分布直方图中,各小长方形的高比为2:3:4:1,那么第二组的频数是( )A、10 B、20 C、15 D、56. 等腰三角形一腰上的高与另一腰的夹角是50°,则这个三角形的底角是( )A、70° B、20° C、70°或20° D、40°或140°7. 如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是( )
A、在AC,BC两边高线的交点处 B、在AC,BC两边中线的交点处 C、在AC,BC两边垂直平分线的交点处 D、在∠A,∠B两内角平分线的交点处5. 已知一个样本容量为50,在频数分布直方图中,各小长方形的高比为2:3:4:1,那么第二组的频数是( )A、10 B、20 C、15 D、56. 等腰三角形一腰上的高与另一腰的夹角是50°,则这个三角形的底角是( )A、70° B、20° C、70°或20° D、40°或140°7. 如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是( )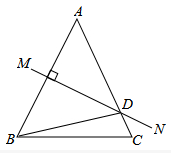 A、30
A、30 B、50
B、50  C、60
C、60  D、65
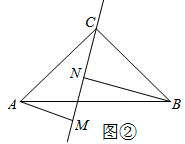
D、65  8. 如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC= ∠ADC=70°,则∠DAO+∠DCO的大小是( )A、70° B、110° C、140° D、150°9. 如图,△ABC的三边AB,BC,CA的长分别为40、50、60,其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO等于 ( )
8. 如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC= ∠ADC=70°,则∠DAO+∠DCO的大小是( )A、70° B、110° C、140° D、150°9. 如图,△ABC的三边AB,BC,CA的长分别为40、50、60,其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO等于 ( )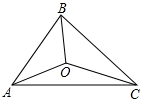 A、1:2:3 B、2:3:4 C、3:4:5 D、4:5:6
A、1:2:3 B、2:3:4 C、3:4:5 D、4:5:6二、填空题
-
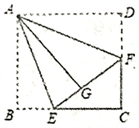
10. 已知2m=4n-1 , 27n=3m-1 , 则n-m=.11. 当x2+2(k-3)x+25是一个完全平方式,则k的值是 .12. 如图,点E、F分别是正方形纸片ABCD的边BC、CD上一点,将正方形纸片ABCD分别沿AE、AF折叠,使得点B、D恰好都落在点G处,且EG=2,DC=6,则FG= .
 13. 如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45 ,则BD的长为 .
13. 如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45 ,则BD的长为 .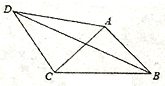
三、解答题
-
14.(1)、计算:
①
②(x-2)(x+5)-x(x+2)
(2)、因式分解:①25x3-36xy2 ②(a2+16b2)2-64a2b2
15. 先化简,再求值:[(x+2y)2-(3x+y)(-y+3x)-5y2]÷(-4x),其中x=- ,y=2.
16. 某小区为了促进全民健身活动的开展,决定在一块面积约为1000 的正方形空地上建一个篮球场,已知篮球场的面积为420 ,其中长是宽的 倍,篮球场的四周必须留出1m宽的空地,请你通过计算说明能否按规定在这块空地上建一个篮球场?
17. “先学后教”课题组对学生参与小组合作的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.课题组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题: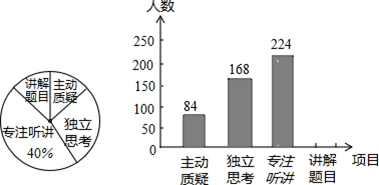 (1)、在这次评价中,一共抽查了名学生;(2)、请将条形统计图补充完整;(3)、求出扇形统计图中,“主动质疑”所对应扇形的圆心角的度数.18. 如图,在△ABC中,AB=AC,点E在CA的延长线上,EP⊥BC,垂足为P,EP交AB于点F,FD∥AC交BC于点D.求证:△AEF是等腰三角形.
(1)、在这次评价中,一共抽查了名学生;(2)、请将条形统计图补充完整;(3)、求出扇形统计图中,“主动质疑”所对应扇形的圆心角的度数.18. 如图,在△ABC中,AB=AC,点E在CA的延长线上,EP⊥BC,垂足为P,EP交AB于点F,FD∥AC交BC于点D.求证:△AEF是等腰三角形.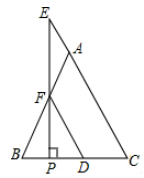 19. 如图,点D在△ABC的AB边上,且∠ACD=∠A.
19. 如图,点D在△ABC的AB边上,且∠ACD=∠A.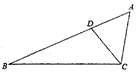 (1)、作∠BDC的平分线DE,交BC于点F(用尺规作图法,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,判断直线DE与直线AC的位置关系,并说明理由.
(1)、作∠BDC的平分线DE,交BC于点F(用尺规作图法,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,判断直线DE与直线AC的位置关系,并说明理由.