河南省商丘市梁园区2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期:2019-01-05 类型:期末考试
一、单选题
-
1. 剪纸是中国民间流行的一种历史悠久的镂空艺术.剪纸的工具材料简便普及,技法易于掌握,有着其他艺术门类不可替代的特性,因而,这一艺术形式从古到今,几乎遍及我国的城镇乡村,深得人民群众的喜爱.下列剪纸图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.00 000 0076克,用科学记数法表示是( )A、7.6×108克 B、7.6×10﹣7克 C、7.6×10﹣8克 D、7.6×10﹣9克3. 下列分式中,最简分式是( )A、
2. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.00 000 0076克,用科学记数法表示是( )A、7.6×108克 B、7.6×10﹣7克 C、7.6×10﹣8克 D、7.6×10﹣9克3. 下列分式中,最简分式是( )A、 B、
B、 C、
C、 D、
D、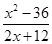 4. 下列运算正确的是( )A、a4•a2=a8 B、a5+a5=a10 C、(﹣3a3)2=6a6 D、(a3)2•a=a75. 图中的两个三角形全等,则 等于( ).
4. 下列运算正确的是( )A、a4•a2=a8 B、a5+a5=a10 C、(﹣3a3)2=6a6 D、(a3)2•a=a75. 图中的两个三角形全等,则 等于( ).
 A、
A、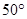 B、
B、 C、
D、
C、
D、 6. 下列式子中,从左到右的变形是因式分解的是( )A、(x﹣1)(x﹣2)=x2﹣3x+2 B、x2﹣3x+2=(x﹣1)(x﹣2) C、x2+4x+4=x(x﹣4)+4 D、x2+y2=(x+y)(x﹣y)7. 如图所示,AB∥CD,O为∠BAC,∠ACD的平分线交点,OE⊥AC于E,若OE=2,则AB与CD之间的距离是( )
6. 下列式子中,从左到右的变形是因式分解的是( )A、(x﹣1)(x﹣2)=x2﹣3x+2 B、x2﹣3x+2=(x﹣1)(x﹣2) C、x2+4x+4=x(x﹣4)+4 D、x2+y2=(x+y)(x﹣y)7. 如图所示,AB∥CD,O为∠BAC,∠ACD的平分线交点,OE⊥AC于E,若OE=2,则AB与CD之间的距离是( ) A、2 B、4 C、6 D、88. 若(a﹣b﹣2)2+|a+b+3|=0,则a2﹣b2的值是( )A、﹣1 B、1 C、6 D、﹣69. 如图,将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B,C,若∠A=40°,求∠ABD+∠ACD=( )
A、2 B、4 C、6 D、88. 若(a﹣b﹣2)2+|a+b+3|=0,则a2﹣b2的值是( )A、﹣1 B、1 C、6 D、﹣69. 如图,将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B,C,若∠A=40°,求∠ABD+∠ACD=( ) A、30° B、40° C、50° D、60°10. 如图,点A,C,D,E在Rt△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD且BC=CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为( )
A、30° B、40° C、50° D、60°10. 如图,点A,C,D,E在Rt△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD且BC=CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为( ) A、30 B、50 C、66 D、80
A、30 B、50 C、66 D、80二、填空题
-
11. 正六边形的每个内角的度数是度.12. 若25x2+kxy+4y2是一个完全平方式,则k= .13. 如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=1,则EF= .
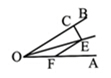 14. 对于实数a、,b,定义运算⊗如下:a⊗b= ,例如:2⊗4=2﹣4= ,计算[2⊗2]×[3⊗2]= .15. 如图,∠AOB=30°,P是∠AOB内一点,PO=10,Q,R分别是OA、OB上的动点,则△PQR周长的最小值为 .
14. 对于实数a、,b,定义运算⊗如下:a⊗b= ,例如:2⊗4=2﹣4= ,计算[2⊗2]×[3⊗2]= .15. 如图,∠AOB=30°,P是∠AOB内一点,PO=10,Q,R分别是OA、OB上的动点,则△PQR周长的最小值为 .
三、解答题
-
16.(1)、因式分解:mx2﹣2mx+m(2)、计算:(2m2n﹣2)2•3m﹣3n3(3)、解分式方程: =117. 先化简,再求值(1)、[(x﹣y)2+(x+y)(x﹣y)]÷2x,其中x=3,y=1.5(2)、( +m﹣2)÷ ,其中m=﹣ .18. 已知:如图,BC∥EF,点C,点F在AD上,AF=DC,BC=EF.求证:△ABC≌△DEF.
 19. 若am=an(a>0且a≠1,m,n是正整数),则m=n.
19. 若am=an(a>0且a≠1,m,n是正整数),则m=n.你能利用上面的结论解决下面的2个问题吗?试试看,相信你一定行!
①如果2×8x×16x=222 , 求x的值;
②如果(27﹣x)2=38 , 求x的值.
20. 如图,Rt△ABC中,∠C=90°,∠A=30°. (1)、作线段AB的垂直平分线DE,垂足为点E,交AC于点D,要求用尺规作图,保留作图痕迹,标注有关字母,不要求写作法和证明;(2)、连接BD,直接写出∠CBD的度数;(3)、如果△BCD的面积为4,请求出△BAD的面积.21. 京九铁路是1992年10月全线开工,1996年9月1日建成通车,是中国一次性建成双线线路最长的一项宏伟铁路工程.其中北京﹣商丘段全长约800千米,京九铁路的通车使商丘成为河南省仅次于郑州的第二大枢纽城市,为商丘提供了发展的机遇.京雄商高铁的预设平均速度将是老京九铁路速度的3倍,可以提前5.8个小时从北京到达商丘,求京雄高铁的平均速度.22. 如图1,在四边形ABCD中,DC∥AB,AD=BC,BD平分∠ABC.
(1)、作线段AB的垂直平分线DE,垂足为点E,交AC于点D,要求用尺规作图,保留作图痕迹,标注有关字母,不要求写作法和证明;(2)、连接BD,直接写出∠CBD的度数;(3)、如果△BCD的面积为4,请求出△BAD的面积.21. 京九铁路是1992年10月全线开工,1996年9月1日建成通车,是中国一次性建成双线线路最长的一项宏伟铁路工程.其中北京﹣商丘段全长约800千米,京九铁路的通车使商丘成为河南省仅次于郑州的第二大枢纽城市,为商丘提供了发展的机遇.京雄商高铁的预设平均速度将是老京九铁路速度的3倍,可以提前5.8个小时从北京到达商丘,求京雄高铁的平均速度.22. 如图1,在四边形ABCD中,DC∥AB,AD=BC,BD平分∠ABC. (1)、求证:AD=DC;(2)、如图2,在上述条件下,若∠A=∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.判断△DEF的形状并证明你的结论.23. 阅读下列材料:
(1)、求证:AD=DC;(2)、如图2,在上述条件下,若∠A=∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.判断△DEF的形状并证明你的结论.23. 阅读下列材料:在学习“分式方程及其解法”过程中,老师提出一个问题:若关于x的分式方程 的解为正数,求a的取值范围?
经过小组交流讨论后,同学们逐渐形成了两种意见:
小明说:解这个关于x的分式方程,得到方程的解为x=a﹣2.由题意可得a﹣2>0,所以a>2,问题解决.
小强说:你考虑的不全面.还必须保证a≠3才行.
老师说:小强所说完全正确.
请回答:小明考虑问题不全面,主要体现在哪里?请你简要说明: .
完成下列问题:
(1)、已知关于x的方程 =1的解为负数,求m的取值范围;(2)、若关于x的分式方程 =﹣1无解.直接写出n的取值范围.24. 在平面直角坐标系中,点A(0,6),B(8,0),AB=10,如图作∠DBO=∠ABO,∠CAy=∠BAO,BD交y轴于点E,直线DO交AC于点C. (1)、①求证:△ACO≌△EDO;②求出线段AC、BD的位置关系和数量关系;(2)、动点P从A出发,沿A﹣O﹣B路线运动,速度为1,到B点处停止运动;动点Q从B出发,沿B﹣O﹣A运动,速度为2,到A点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作PE⊥CD于点E,QF⊥CD于点F.问两动点运动多长时间时△OPE与△OQF全等?
(1)、①求证:△ACO≌△EDO;②求出线段AC、BD的位置关系和数量关系;(2)、动点P从A出发,沿A﹣O﹣B路线运动,速度为1,到B点处停止运动;动点Q从B出发,沿B﹣O﹣A运动,速度为2,到A点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作PE⊥CD于点E,QF⊥CD于点F.问两动点运动多长时间时△OPE与△OQF全等?