河南省平顶山市2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期:2019-01-05 类型:期末考试
一、单选题
-
1. 在 , , , 中,是最简二次根式的是( )A、 B、
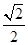 C、
C、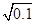 D、
D、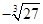 2. 4的平方根是( )A、±2 B、2 C、 ±
2. 4的平方根是( )A、±2 B、2 C、 ±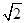 D、
D、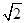 3. 点 在平面直角坐标系的 轴上,则点A关于y轴对称点的坐标为( )A、(-4,0) B、(0,-4) C、(4,0) D、(0,4)4. 某一次函数的图象经过点(1,2),且y随x的增大而减小,则这个函数的表达式可能是( )A、y=2x+4 B、y=3x-1 C、y=-3x+1 D、y=-2x+45. 下列命题正确的是( )A、如果两个角相等那么它们是对顶角 B、如果a=b,那么|a|=|b| C、面积相等的两个三角形全等 D、如果 ,那么a=b6. 如图所示是小明在某条道路所统计的某个时段来往车辆的车速情况,下列说法中正确的是( )
3. 点 在平面直角坐标系的 轴上,则点A关于y轴对称点的坐标为( )A、(-4,0) B、(0,-4) C、(4,0) D、(0,4)4. 某一次函数的图象经过点(1,2),且y随x的增大而减小,则这个函数的表达式可能是( )A、y=2x+4 B、y=3x-1 C、y=-3x+1 D、y=-2x+45. 下列命题正确的是( )A、如果两个角相等那么它们是对顶角 B、如果a=b,那么|a|=|b| C、面积相等的两个三角形全等 D、如果 ,那么a=b6. 如图所示是小明在某条道路所统计的某个时段来往车辆的车速情况,下列说法中正确的是( )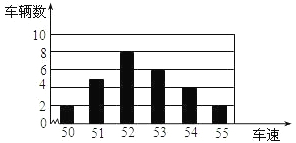 A、中位数是52.5 B、众数是8 C、众数是52 D、中位数是537. 如图,小亮从家步行到公交车站台,乘公交车去学校. 图中的折线表示小亮的离家距离s(km)与所花时间t(min)之间的函数关系. 下列说法错误的是( )
A、中位数是52.5 B、众数是8 C、众数是52 D、中位数是537. 如图,小亮从家步行到公交车站台,乘公交车去学校. 图中的折线表示小亮的离家距离s(km)与所花时间t(min)之间的函数关系. 下列说法错误的是( )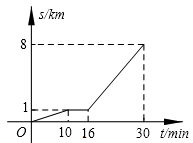 A、他离家8km共用了30min B、公交车的速度是350m/min C、他步行的速度是100m/min D、他等公交车时间为6min8. 如图,所有的四边形是正方形,所有的三角形都是直角三角形,其中最大的正方形边长为13 cm,则图中所有的正方形的面积之和为( )
A、他离家8km共用了30min B、公交车的速度是350m/min C、他步行的速度是100m/min D、他等公交车时间为6min8. 如图,所有的四边形是正方形,所有的三角形都是直角三角形,其中最大的正方形边长为13 cm,则图中所有的正方形的面积之和为( )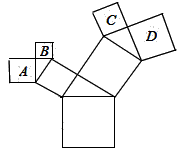 A、169cm2 B、196cm2 C、338cm2 D、507cm29. 我校举行春季运动会系列赛中,九年级(1)班、(2)班的竞技实力相当,关于比赛结果,
A、169cm2 B、196cm2 C、338cm2 D、507cm29. 我校举行春季运动会系列赛中,九年级(1)班、(2)班的竞技实力相当,关于比赛结果,甲同学说:(1)班与(2)班的得分为6:5;
乙同学说:(1)班的得分比(2)班的得分的2倍少40分;
若设(1)班的得分为x分,(2)班的得分为y分,根据题意所列方程组应为( )
A、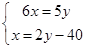 B、
B、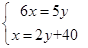 C、
C、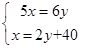 D、
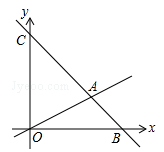
D、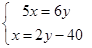 10. 如图,在平面直角坐标系xOy中,已知正比例函数 与一次函数 的图象交于点A.设x轴上一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交 和 的图象于点B、C.若 ,则 的值为( )
10. 如图,在平面直角坐标系xOy中,已知正比例函数 与一次函数 的图象交于点A.设x轴上一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交 和 的图象于点B、C.若 ,则 的值为( )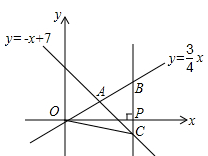 A、8 B、6 C、5 D、4
A、8 B、6 C、5 D、4二、填空题
-
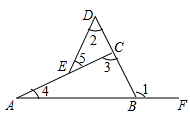
11. 计算: = .12. 如图,在△ABC中,∠1是它的外角,E为边AC上一点,延长BC到D,连接DE,则∠1∠2(填“>”, “<”, “=”)
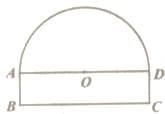
 13. 数轴上与原点相距 个单位长度的点,它所表示的数为.14. 如图,四边形ABCD是正方形,直线l1、l2、l3分别过A、B、C三点,l1∥l2∥l3 , 若l1与l2之间的距离为4,l2与l3之间的距离为5,则正方形的边长为.
13. 数轴上与原点相距 个单位长度的点,它所表示的数为.14. 如图,四边形ABCD是正方形,直线l1、l2、l3分别过A、B、C三点,l1∥l2∥l3 , 若l1与l2之间的距离为4,l2与l3之间的距离为5,则正方形的边长为.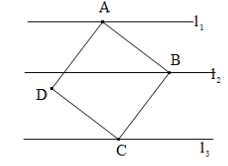 15. 利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是cm.
15. 利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是cm.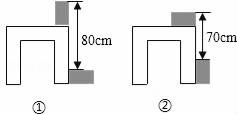
三、解答题
-
16. 计算(1)、(2)、17. 如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为A(-4,5),C(-1,3).
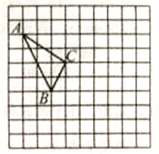 (1)、①请在网格平面内作出平面直角坐标系(不写作法);
(1)、①请在网格平面内作出平面直角坐标系(不写作法);②请作出△ABC关于y轴对称△A'B'C';
(2)、分别写出A'、B'、C'的坐标.18. 实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.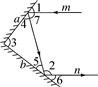 (1)、如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射.若被b反射出的光线n与光线m平行,且∠1=50°,则∠2= , ∠3=;(2)、在(1)中,若∠1=55°,则∠3=;若∠1=40°,则∠3=;(3)、由(1)、(2)请你猜想:当两平面镜a,b的夹角∠3等于多少度时,可以使任何射到平面镜a上的光线m,经过平面镜a,b的两次反射后,入射光线m与反射光线n平行,请说明理由.19. 夏季来临,天气逐渐炎热起来.某商店将某种碳酸饮料每瓶的价格上调了10%,将某种果汁饮料每瓶的价格下调了5%.已知调价前买这两种饮料各一瓶共花费7元,调价后买上述碳酸饮料3瓶和果汁饮料2瓶共花费17.5元,问这两种饮料在调价前每瓶各多少元?20. 甲乙两名运动员进行射击选拨赛,每人射击10次,其中射击中靶情况如下表:
(1)、如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射.若被b反射出的光线n与光线m平行,且∠1=50°,则∠2= , ∠3=;(2)、在(1)中,若∠1=55°,则∠3=;若∠1=40°,则∠3=;(3)、由(1)、(2)请你猜想:当两平面镜a,b的夹角∠3等于多少度时,可以使任何射到平面镜a上的光线m,经过平面镜a,b的两次反射后,入射光线m与反射光线n平行,请说明理由.19. 夏季来临,天气逐渐炎热起来.某商店将某种碳酸饮料每瓶的价格上调了10%,将某种果汁饮料每瓶的价格下调了5%.已知调价前买这两种饮料各一瓶共花费7元,调价后买上述碳酸饮料3瓶和果汁饮料2瓶共花费17.5元,问这两种饮料在调价前每瓶各多少元?20. 甲乙两名运动员进行射击选拨赛,每人射击10次,其中射击中靶情况如下表:第一次
第二次
第三次
第四次
第五次
第六次
第七次
第八次
第九次
第十次
甲
7
10
8
10
9
9
10
8
10
9
乙
10
7
10
9
9
10
8
10
7
10
(1)、选手甲的成绩的中位数是分;选手乙的成绩的众数是分;(2)、计算选手甲的平均成绩和方差;(3)、已知选手乙的成绩的方差是1.4,则成绩较稳定的是哪位选手?(直按写出结果)21. 认真阅读下面关于三角形内外角平分线的研究片段,完成所提出的问题.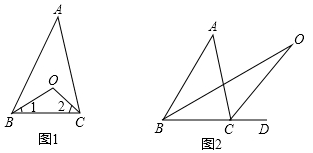
探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+ ∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线,∴∠1= ∠ABC,∠2= ∠ACB.
∴∠1+∠2= (∠ABC+∠ACB)= (180°-∠A)=90°- ∠A.
∴∠BOC=180°-(∠1+∠2)=180°-(90°- ∠A)=90°+ ∠A
探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.