河南省南召县2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期:2019-01-05 类型:期末考试
一、单选题
-
1. 若代数式 有意义,则实数 的取值范围是( )A、
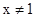 B、
B、 C、
C、 D、
D、 2. 计算 的正确结果是( )A、
2. 计算 的正确结果是( )A、 B、
B、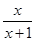 C、
C、 D、
D、 3. 一次函数 的图象经过点A、
3. 一次函数 的图象经过点A、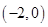 B、
B、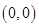 C、
D、
C、
D、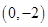 4. 点 在反比例函数 的图象上,则下列各点在此函数图象上的是A、
4. 点 在反比例函数 的图象上,则下列各点在此函数图象上的是A、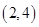 B、
B、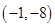 C、
C、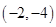 D、
D、 5. 四边形 中,对角线 、 相交于点 ,下列条件不能判定这个四边形是平行四边形的是( )
5. 四边形 中,对角线 、 相交于点 ,下列条件不能判定这个四边形是平行四边形的是( ) A、AB∥DC,AD∥BC B、AO=CO,BO=DO C、AB∥DC,AD=BC D、AB=DC,AD=BC6. 我市某一周的日最高气温统计如下表:
A、AB∥DC,AD∥BC B、AO=CO,BO=DO C、AB∥DC,AD=BC D、AB=DC,AD=BC6. 我市某一周的日最高气温统计如下表:最高气温(℃)
25
26
27
28
天数
1
1
2
3
则该周的日最高气温的中位数与众数分别是( )
A、26.5,27 B、27,28 C、27,27 D、27.5,287. 在今年的中招体育考试中,我校甲、乙、丙、丁四个班级的平均分完全一样,方差分别为:S甲2=8.5,S乙2=21.7,S丙2=15,S丁2=17,则四个班体考成绩最稳定的是( )A、甲班 B、乙班 C、丙班 D、丁班8. 如图,小聪在作线段 的垂直平分线时,他是这样操作的:分别以 和 为圆心,大于 的长为半径画弧,两弧相交于 , ,则直线 即为所求.根据他的作图方法可知四边形 一定是( ) A、矩形 B、菱形 C、正方形 D、无法确定9. 如图,已知菱形 的对角线 , 的长分别为6cm,8cm, 于点 ,则 的长是( )
A、矩形 B、菱形 C、正方形 D、无法确定9. 如图,已知菱形 的对角线 , 的长分别为6cm,8cm, 于点 ,则 的长是( ) A、
A、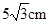 B、
B、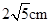 C、
C、 D、
D、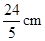 10. 如图1,在矩形 中,动点 从点 出发,沿 方向运动至点 处停止,设点 运动的路程为 ,△BCE的面积为 ,如果 关于 的函数图象如图2所示,则当 时,点 应运动到( )
10. 如图1,在矩形 中,动点 从点 出发,沿 方向运动至点 处停止,设点 运动的路程为 ,△BCE的面积为 ,如果 关于 的函数图象如图2所示,则当 时,点 应运动到( )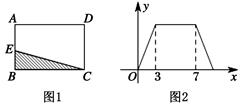 A、 点
A、 点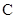 处
B、 点
处
B、 点 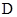 处
C、 点
处
C、 点 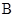 处
D、 点
处
D、 点 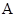 处
处
二、填空题
-
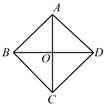
11. 化简: 的结果是 .12. 如图,在四边形 中, ,对角线 与 相交于点 ,若不增加任何字母与辅助线,要使四边形 是正方形,则还需增加一个条件是 .
 13. 某食堂午餐供应10元、16元、20元三种价格的盒饭,根据食堂某月销售午餐盒饭的统计图,可计算出该月食堂午餐盒饭的平均价格是元.
13. 某食堂午餐供应10元、16元、20元三种价格的盒饭,根据食堂某月销售午餐盒饭的统计图,可计算出该月食堂午餐盒饭的平均价格是元.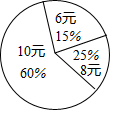 14. 当 时,不论k取任何实数,函数 的值为3,所以直线 一定经过定点 ;同样,直线 一定经过的定点为 .15. 如图,正方形 的顶点 , 分别在 轴, 轴上, 是菱形 的对角线,若 , ,则点E的坐标是 .
14. 当 时,不论k取任何实数,函数 的值为3,所以直线 一定经过定点 ;同样,直线 一定经过的定点为 .15. 如图,正方形 的顶点 , 分别在 轴, 轴上, 是菱形 的对角线,若 , ,则点E的坐标是 .
三、解答题
-
16. 化简: ,然后在不等式x≤2的非负整数解中选择一个适当的数代入求值.17. 解方程: .18. 某市团委举行以“我的中国梦”为主题的知识竞赛,甲、乙两所学校的参赛人数相等,比赛结束后,发现学生成绩分别为 分, 分, 分, 分,并根据统计数据绘制了如下不完整的统计图表:
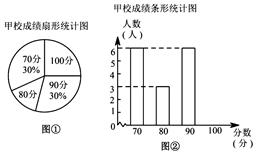
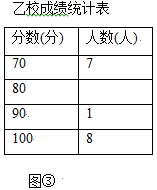 (1)、乙学校的参赛人数是人;(2)、在图①中,“ 分”所在扇形的圆心角度数为;(3)、请你将图②补充完整;(4)、求乙校成绩的平均分;19. 如图, 、 是四边形 的对角线 上两点, ,DF∥BE, .求证:四边形 是平行四边形.
(1)、乙学校的参赛人数是人;(2)、在图①中,“ 分”所在扇形的圆心角度数为;(3)、请你将图②补充完整;(4)、求乙校成绩的平均分;19. 如图, 、 是四边形 的对角线 上两点, ,DF∥BE, .求证:四边形 是平行四边形.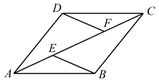 20. 如图,在平面直角坐标系中,正方形 的顶点 与坐标原点重合,点 的坐标为 ,点 在 轴的负半轴上,点 , 分别在边 , 上,且 , ,一次函数 的图象过点 和 ,反比例函数 的图象经过点 ,且与 的交点为 .
20. 如图,在平面直角坐标系中,正方形 的顶点 与坐标原点重合,点 的坐标为 ,点 在 轴的负半轴上,点 , 分别在边 , 上,且 , ,一次函数 的图象过点 和 ,反比例函数 的图象经过点 ,且与 的交点为 . (1)、直接写出反比例函数解析式一次函数的解析式;(2)、若点 在直线 上,且使△OPM的面积与四边形 的面积相等,求点 的坐标.21. 随着“互联网 ”时代的到来,一种新型打车方式受到大众欢迎 该打车方式的计价规则如图 所示,若车辆以平均速度 行驶了skm , 则打车费用为 元 不足9元按9元计价 小明某天用该打车方式出行,按上述计价规则,其打车费用 元 与行驶里程 的函数关系也可由如图 表示.
(1)、直接写出反比例函数解析式一次函数的解析式;(2)、若点 在直线 上,且使△OPM的面积与四边形 的面积相等,求点 的坐标.21. 随着“互联网 ”时代的到来,一种新型打车方式受到大众欢迎 该打车方式的计价规则如图 所示,若车辆以平均速度 行驶了skm , 则打车费用为 元 不足9元按9元计价 小明某天用该打车方式出行,按上述计价规则,其打车费用 元 与行驶里程 的函数关系也可由如图 表示.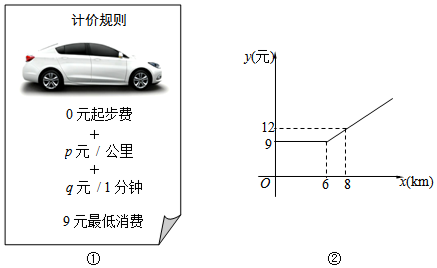 (1)、当 时,求y与x的函数关系式.(2)、若 , ,求该车行驶的平均速度.22. 如图,在平面直角坐标系中,正比例函数 与反比例函数 的图象分别交于 , 两点,已知点 与点 关于坐标原点 成中心对称,且点 的坐标为 .其中 .
(1)、当 时,求y与x的函数关系式.(2)、若 , ,求该车行驶的平均速度.22. 如图,在平面直角坐标系中,正比例函数 与反比例函数 的图象分别交于 , 两点,已知点 与点 关于坐标原点 成中心对称,且点 的坐标为 .其中 .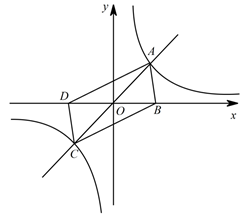 (1)、四边形 是 . (填写四边形 的形状)(2)、当点 的坐标为 时,且四边形 是矩形,求 , 的值.(3)、试探究:随着 与 的变化,四边形 能不能成为菱形?若能,请直接写出 的值;若不能,请说明理由.
(1)、四边形 是 . (填写四边形 的形状)(2)、当点 的坐标为 时,且四边形 是矩形,求 , 的值.(3)、试探究:随着 与 的变化,四边形 能不能成为菱形?若能,请直接写出 的值;若不能,请说明理由.