河南省南阳市南召县2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期:2019-01-05 类型:期末考试
一、单选题
-
1. ﹣1的相反数是( )A、 1-
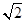 B、
B、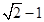 C、
C、 D、
D、 2. 下列运算正确的是( )A、3a•4a=12a B、(a3)2=a6 C、(﹣2a)3=﹣2a3 D、a12÷a3=a43. 八年级某班40名学生的数学测试成绩分为5组,第1﹣4组的频数分别为12,10,6,8,则第5组的频率是( )A、0.1 B、0.2 C、0.3 D、0.44. 用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( )
2. 下列运算正确的是( )A、3a•4a=12a B、(a3)2=a6 C、(﹣2a)3=﹣2a3 D、a12÷a3=a43. 八年级某班40名学生的数学测试成绩分为5组,第1﹣4组的频数分别为12,10,6,8,则第5组的频率是( )A、0.1 B、0.2 C、0.3 D、0.44. 用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( )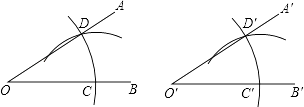 A、(SAS) B、(SSS) C、(ASA) D、(AAS)5. 某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( )
A、(SAS) B、(SSS) C、(ASA) D、(AAS)5. 某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( ) A、25人 B、35人 C、40人 D、100人6. 若x2+kx+25是完全平方式,则k的值是( )A、﹣10 B、10 C、5 D、10或﹣107. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( )
A、25人 B、35人 C、40人 D、100人6. 若x2+kx+25是完全平方式,则k的值是( )A、﹣10 B、10 C、5 D、10或﹣107. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( ) A、0.7米 B、1.5米 C、2.2米 D、2.4米8. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( )
A、0.7米 B、1.5米 C、2.2米 D、2.4米8. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( )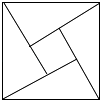 A、3 B、4 C、5 D、69.
A、3 B、4 C、5 D、69.园丁住宅小区有一块草坪如图所示.已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是( )
 A、24米2 B、36米2 C、48米2 D、72米2
A、24米2 B、36米2 C、48米2 D、72米2二、填空题
-
10. 计算: = .11. 把命题“角平分线上的点到这个角两边的距离相等”改写成“如果…,那么…、”的形式:如果 , 那么 .12. 为说明命题“如果a>b,那么 ”是假命题,你举出的反例是 .13.
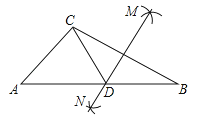
如图,在△ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于M,N两点;
②作直线MN交AB于点D,连接CD,若CD=AC,∠B=25°,则∠ACB的度数为 .
 14. 如图,有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于 AC的射线AX上运动,当AP=时,才能使△ABC与△QPA全等.
14. 如图,有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于 AC的射线AX上运动,当AP=时,才能使△ABC与△QPA全等.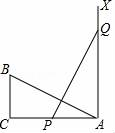
三、解答题
-
15. 四个数a,b,c,d排列成 ,我们称之为二阶行列式,规定它的运算法则为 =ad﹣bc,若 =12,求x值.16. 先化简,再求值:(2a﹣1)2﹣2(a+1)(a﹣1)﹣a(a﹣2),其中1﹣a2+2a=0.17. 某商场对一种新售的手机进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(不比较喜欢)、D(非常喜欢)四个等级对该手机进行评价,图①和图②是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题:
 (1)、本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.(2)、图①中,a等于多少?D等级所占的圆心角为多少度?18. 计算(1)、计算:(a﹣b)(a2+ab+b2)(2)、利用所学知识以及(1)所得等式,分解因式:m3﹣n3﹣3mn(m﹣n)19. 如图,点C,F,E,B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,写出CD与AB之间的关系,并证明你的结论.
(1)、本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.(2)、图①中,a等于多少?D等级所占的圆心角为多少度?18. 计算(1)、计算:(a﹣b)(a2+ab+b2)(2)、利用所学知识以及(1)所得等式,分解因式:m3﹣n3﹣3mn(m﹣n)19. 如图,点C,F,E,B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,写出CD与AB之间的关系,并证明你的结论. 20. 已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
20. 已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点. (1)、求证:△ACE≌△BCD;(2)、求证:2CD2=AD2+DB2 .21.(1)、问题发现
(1)、求证:△ACE≌△BCD;(2)、求证:2CD2=AD2+DB2 .21.(1)、问题发现
如图①,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上,请直接写出线段BE与线段CD的数量关系:;
(2)、操作探究如图②,将图①中的△ABC绕点A顺时针旋转,旋转角为α(0<α<360),请判断线段BE与线段CD的数量关系,并说明理由.
22. 如图,在长方形ABCD中,AB:BC=3:4,AC=5,点P从点A出发,以每秒1个单位的速度,沿△ABC边A→B→C→A的方向运动,运动时间为t秒. (1)、求AB与BC的长;(2)、在点P的运动过程中,是否存在这样的点P,使△CDP为等腰三角形?若存在,求出t值;若不存在,说明理由.
(1)、求AB与BC的长;(2)、在点P的运动过程中,是否存在这样的点P,使△CDP为等腰三角形?若存在,求出t值;若不存在,说明理由.