河南省洛阳市嵩县2017-2018学年八年级上学期数学期末考试试卷

试卷更新日期：2019-01-05 类型：期末考试

进入出卷网下载

一、单选题

1. 若一个数的平方根是±8，则这个数的立方根是（）

A、±2 B、±4 C、2 D、4

查看试题解析
2. 下列运算，正确的是（）

A、a²•a³=a⁶ B、（a²）³=a⁶ C、a¹⁰÷a²=a⁵ D、a+a³=a⁴

查看试题解析
3. 若等腰三角形的周长为10 cm，其中一边长为2 cm，则该等腰三角形的底边长为（）

A、2 cm B、4 cm C、6 cm D、8 cm

查看试题解析
4. 等边三角形的边长为2，则该三角形的面积为（）

A、 B、 C、 D、3

查看试题解析
5. 一座建筑物发生了火灾，消防车到达现场后，发现最多只能靠近建筑物底端5米，消防车的云梯最大升长为13米，则云梯可以达到该建筑物的最大高度是（）

A、12米 B、13米 C、14米 D、15米

查看试题解析
6. 如图，△ABC中，∠C=90°，∠CAB=50°．按以下步骤作图：
①以点A为圆心，小于AC长为半径画弧，分别交AB，AC于点E，F；②分别以点E，F为圆心，大于 $\frac{1}{2}$ EF长为半径画弧，两弧相交于点G；③作射线AG交BC边于点D．则∠ADC的度数为（）

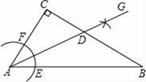A、65° B、60° C、55° D、45°

查看试题解析
7. 如图，Rt△ABC中，∠ACB=90°，若AB=15cm，则正方形ADEC和正方形BCFG的面积和为（）

A、150cm² B、200cm² C、225cm² D、无法计算

查看试题解析
8.
武汉市光谷实验中学九（1）班为了了解全班学生喜欢球类活动的情况，采取全面调查的方法，从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好，根据调查的结果组建了4个兴趣小组，并绘制成如图所示的两幅不完整的统计图（如图①，②，要求每位学生只能选择一种自己喜欢的球类），下列说法错误的是（　　）

A、九（1）班的学生人数为40 B、m的值为10 C、n的值为20 D、表示“足球”的扇形的圆心角是70°

查看试题解析
9. 如图，在△ABC中，AB=4，AC=6，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC分别交AB，AC于M，N，则△AMN的周长为（）

A、10 B、6 C、4 D、不确定

查看试题解析
10. 如图，在△ABC中，∠A=36°，AB=AC，CD，BE分别是∠ACB，∠ABC的平分线，CD、BE相交于F点，连接DE，则图中全等的三角形有多少组（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

11. 如果（x+1）（x+m）的乘积中不含x的一次项，则m的值为．

查看试题解析
12. 当a+b=3，x﹣y=1时，代数式a²+2ab+b²﹣x+y的值等于．

查看试题解析
13. 若3 ^x＝10, 3 ^y＝5，则3^2x—y= ．

查看试题解析
14. 写出命题：“直角都相等”的逆命题：．

查看试题解析
15. 如图所示，AOB是一钢架，且∠AOB=10°，为了使钢架更加坚固，需在其内部添加一些钢管EF，FG，GH…，添加的钢管长度都与OE相等，则最多能添加这样的钢管根．

查看试题解析

三、解答题

16. 计算

(1)、 $\sqrt[3]{- 27} + \sqrt{{(- 3)}^{2}} - \sqrt[3]{-} 1$

(2)、化简与求值：[（x﹣2y）²+（x﹣2y）（x+2y）﹣2x（2x﹣y）]÷2x，其中x=5，y=﹣6

查看试题解析
17. 在日常生活中，如取款、上网等都需要密码．有一种用“因式分解”法产生的密码，方便记忆．原理是：如对于多项式x⁴－y⁴ ，因式分解的结果是(x－y)(x＋y)·(x²＋y²)，若取x＝9，y＝9时，则各个因式的值是：(x－y)＝0，(x＋y)＝18，x²＋y²＝162，于是就可以把“018162”作为一个六位数的密码．对于多项式4x³－xy² ，取x＝10，y＝10时，请你写出用上述方法产生的密码．

查看试题解析
18. 如图，一块大的三角板ABC，D是AB上一点，现要求过点D割出一块小的三角板ADE，使∠ADE=∠ABC，

(1)、尺规作出∠ADE．（不写作法，保留作图痕迹，要写结论）

(2)、判断BC与DE是否平行，如果是，请证明．

查看试题解析
19. 已知：如图，OM是∠AOB的平分线，C是OM上一点，且CD⊥OA于D，CE⊥OB于E，AD=EB．求证：AC=CB．

查看试题解析
20. 如图，在四边形ABCD中，AB=AD=4，∠A=60°，BC=4 $\sqrt{5}$ ，CD=8．

(1)、求∠ADC的度数；

(2)、求四边形ABCD的面积

查看试题解析

21. 为了提高学生书写汉字的能力，增强保护汉子的意识，某校举办了首届“汉字听写大赛”，学生经选拔后进入决赛，测试同时听写100个汉字，每正确听写出一个汉字得1分，本次决赛，学生成绩为

x

（分），且

50 \leq x < 100

，将其按分数段分为五组，绘制出以下不完整表格：

组别	成绩 $x$ （分）	频数（人数）	频率
一	$50 \leq x < 60$	2	0.04
二	$60 \leq x < 70$	10	0.2
三	$70 \leq x < 80$	14	b
四	$80 \leq x < 90$	a	0.32
五	$90 \leq x < 100$	8	0.16

请根据表格提供的信息，解答以下问题：

(1)、本次决赛共有名学生参加；

(2)、直接写出表中a= ， b=；

(3)、请补全下面相应的频数分布直方图；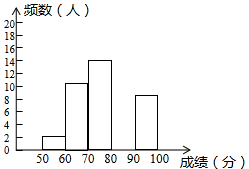

(4)、若决赛成绩不低于80分为优秀，则本次大赛的优秀率为。

查看试题解析

22. 如图，已知△ABC中，∠B=90°，AB=16cm，BC=12cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．

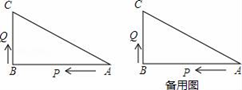(1)、出发2秒后，求PQ的长；

(2)、当点Q在边BC上运动时，出发几秒钟后，△PQB能形成等腰三角形？

(3)、当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．

查看试题解析
23. 如图，△ABC是等边三角形，D为BC边上一个动点（D与B、C均不重合），AD=AE，∠DAE=60°，连接CE．

(1)、求证：△ABD≌△ACE；

(2)、求证：CE平分∠ACF；

(3)、若AB=2，当四边形ADCE的周长取最小值时，求BD的长．

查看试题解析