浙江省温州市龙湾区2018届数学中考二模试卷

试卷更新日期：2019-01-05 类型：中考模拟

进入 出卷网 下载

一、单选题

  • 1. a是不为零的自然数，a与 1a 的关系一定是（   ）
    A、 a≥ B、 a＜ C、 a= D、 a＞

    查看试题解析

  • 2. 如图是由若干个大小相同的小正方体堆砌而成的几何体，那么其三种视图中面积最小的是（   ）

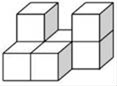    A、主视图 B、俯视图 C、左视图 D、一样大

    查看试题解析

  • 3. 下面的统计图反映了我市2011﹣2016年气温变化情况，下列说法不合理的是（   ）

    A、2011﹣2014年最高温度呈上升趋势 B、2014年出现了这6年的最高温度 C、2011﹣2015年的温差成下降趋势 D、2016年的温差最大

    查看试题解析

  • 4. 已知点A（﹣3，m）与点B（2，n）是直线y=﹣2x+b上的两点，则m与n的大小关系是（   ）
    A、m＜n B、m=n C、m＞n D、无法确定

    查看试题解析

  • 5. 如图，⊙O的直径AB与弦CD垂直相交于点E，且AC=2，AE= 3 ．则 BD⌢  的长是（   ）

    A、 B、 C、 D、

    查看试题解析

  • 6. 用配方法解一元二次方程x2﹣6x﹣1=0时，下列变形正确的是（   ）
    A、（x﹣3）2=1 B、（x﹣3）2=10 C、（x+3）2=1 D、（x+3）2=10

    查看试题解析

  • 7. 如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E，若∠E=35°，则∠BAC的度数为（     ）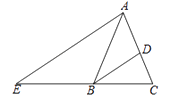

    A、40° B、45° C、50° D、55°

    查看试题解析

  • 8. “五一”江北水城文化旅游节期间，几名同学包租一辆面包车前去旅游，面包车的租价为180元，出发时又增加了两名同学，结果每个同学比原来少摊了3元钱车费，设实际参加游览的同学共x人，则所列方程为（   ）
    A、 B、 C、 D、

    查看试题解析

  • 9.

    如图所示为一种“羊头”形图案，其作法是：从正方形①开始，以它的一边为斜边，向外作等腰直角三角形，然后再以其直角边为边，分别向外作正方形②和②，…，依此类推，若正方形①的面积为64，则正方形⑤的面积为（　　）

    A、2 B、4 C、8 D、16

    查看试题解析

  • 10. 如图，已知矩形ABCD，AB=4，AD=2，E为AB的中点，连接DE与AC交于点F，则CF的长等于（   ）

    A、 B、 C、 D、

    查看试题解析

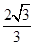
二、填空题

  • 11. 化简：a+1+a（a+1）+a（a+1）2+…+a（a+1）99= ．

    查看试题解析

  • 12. 已知m＞6，则关于x的不等式（6﹣m）x＜m﹣6的解集为

    查看试题解析

  • 13. 袋子中装有红、黄、绿三种颜色的小球各一个，从中任意摸出一个放回搅匀，再摸出一个球，则两次摸出的球都是黄色的概率是 ．

    查看试题解析

  • 14. 如图，将Rt△ABC的BC边绕C旋转到CE的位置，且在Rt△ABC中，∠B=90°，∠A=30°，则∠ACD=度．

    查看试题解析

  • 15. 有一座抛物线形拱桥，正常水位时桥下水面宽度为20米，拱顶距离水面4米．设正常水位时桥下的水深为2米，为保证过往船只顺利航行，桥下水面的宽度不得小于18米，则水深超过米时就会影响过往船只在桥下的顺利航行．

    查看试题解析

  • 16. 如图，点A是反比例函数y= 5x （x＞0）图象上的一点，点B是反比例函数y=﹣ 1x （x＜0）图象上的点，连接OA、OB、AB，若∠AOB=90°，则sin∠A=

    查看试题解析

三、解答题

  • 17.    
    (1)、计算： (−2)−1+(3−1)0 ﹣sin30°
    (2)、化简： a+1a2−a+1a .

    查看试题解析

  • 18. 如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．

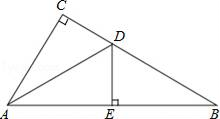    (1)、求证：△ACD≌△AED；
    (2)、若∠B=30°，CD=2，求BD的长．

    查看试题解析

  • 19. 如图所示，正方形网格中，每个小正方形的边长是1个单位长度

    ①在图中作出△ABC关于点O对称的△A1B1C1（不写作法，但需在图中标注相应字母）；

    ②已知点A、B的坐标分别为A（﹣4，4）、B（﹣3，1），求点C1的坐标．

    查看试题解析

  • 20. 某工厂车间共有10名工人，调查每个工人的日均生产能力，获得数据制成如下统计图．

    (1)、求这10名工人的日均生产件数的平均数、众数、中位数；
    (2)、若要使占60%的工人都能完成任务，应选什么统计量（平均数、中位数、众数）做日生产件数的定额？

    查看试题解析

  • 21. 如图，AB为⊙O的直径，点C为⊙O上一点，将弧BC沿直线BC翻折，使弧BC的中点D恰好与圆心O重合，连接OC，CD，BD，过点C的切线与线段BA的延长线交于点P，连接AD，在PB的另一侧作∠MPB=∠ADC．

    (1)、判断PM与⊙O的位置关系，并说明理由；
    (2)、若PC= 3 ，求四边形OCDB的面积．

    查看试题解析

  • 22. 已知抛物线y=ax2经过点A（﹣2，﹣8）．
    (1)、求此抛物线的函数解析式；
    (2)、写出这个二次函数图象的顶点坐标、对称轴；
    (3)、判断点B（﹣1，﹣4）是否在此抛物线上；
    (4)、求出此抛物线上纵坐标为﹣6的点的坐标．

    查看试题解析

  • 23. 如图，在平面直角坐标系中，菱形ABCD的边AB在x轴上，点B坐标（﹣3，0），点C在y轴正半轴上，且sin∠CBO= 45 ，点P从原点O出发，以每秒一个单位长度的速度沿x轴正方向移动，移动时间为t（0≤t≤5）秒，过点P作平行于y轴的直线l，直线l扫过四边形OCDA的面积为S．

    (1)、求点D坐标．
    (2)、求S关于t的函数关系式．
    (3)、在直线l移动过程中，l上是否存在一点Q，使以B、C、Q为顶点的三角形是等腰直角三角形？若存在，直接写出Q点的坐标；若不存在，请说明理由．

    查看试题解析

  • 24. 如图，△ABC内接于⊙O，弦CD平分∠ACB，点E为弧AD上一点，连接CE、DE，CD与AB交于点N．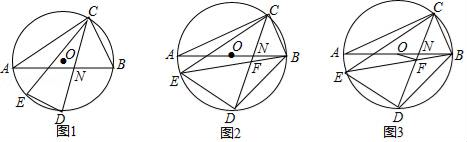

    (1)、如图1，求证：∠AND=∠CED；
    (2)、如图2，AB为⊙O直径，连接BE、BD，BE与CD交于点F，若2∠BDC=90°﹣∠DBE，求证：CD=CE；
    (3)、如图3，在（2）的条件下，连接OF，若BE=BD+4，BC= 210 ，求线段OF的长．

    查看试题解析