山东省临沂市2018-2019学年高三上学期文数期中考试试卷
试卷更新日期:2019-01-05 类型:期中考试
一、单选题
-
1. 已知集合A={x|﹣2<x<3},B={x|log2x>0},则A∩B=( )A、(﹣2,1) B、(0,1) C、(0,3) D、(1,3)2. 设命题p:∃x0∈(0,+∞), ≤x02 , 则命题p的否定为( )A、∀x∈(0,+∞),
 ≥x2
B、∀x∈(0,+∞),
≥x2
B、∀x∈(0,+∞),  ≤x2
C、∀x∈(0,+∞),
≤x2
C、∀x∈(0,+∞),  >x2
D、∀x∈(0,+∞),
>x2
D、∀x∈(0,+∞),  <x2
3. 已知等差数列{an}的前n项和为Sn , 若a2+a6=14,则S7=( )A、13 B、35 C、49 D、634. 已知实数x,y满足x3<y3 , 则下列不等式中恒成立的是( )A、( )x>( )y B、ln(x2+1)>ln(y2+1) C、
<x2
3. 已知等差数列{an}的前n项和为Sn , 若a2+a6=14,则S7=( )A、13 B、35 C、49 D、634. 已知实数x,y满足x3<y3 , 则下列不等式中恒成立的是( )A、( )x>( )y B、ln(x2+1)>ln(y2+1) C、 D、tanx>tany
5. 在直角坐标系中,若角α的终边经过点P(sin ,cos ),则cos( +α)=( )A、 B、﹣ C、 D、﹣6. 将函数y=2sin(2x﹣ )的图象向左平移 个单位长度,所得图象的一个对称中心为( )A、( ,0) B、(
D、tanx>tany
5. 在直角坐标系中,若角α的终边经过点P(sin ,cos ),则cos( +α)=( )A、 B、﹣ C、 D、﹣6. 将函数y=2sin(2x﹣ )的图象向左平移 个单位长度,所得图象的一个对称中心为( )A、( ,0) B、(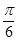 ,0)
C、(
,0)
C、( 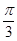 ,0)
D、(
,0)
D、(  ,0)
7. 定义符号函数sgnx ,则函数f(x)=x2sgnx的图象大致是( )A、
,0)
7. 定义符号函数sgnx ,则函数f(x)=x2sgnx的图象大致是( )A、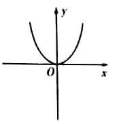 B、
B、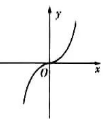 C、
C、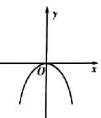 D、
D、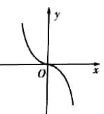 8. 在平行四边形ABCD中,设 ,则 =( )A、
8. 在平行四边形ABCD中,设 ,则 =( )A、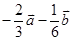 B、
B、 C、
C、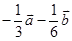 D、
D、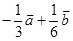 9. 已知函数f(x)是定义域为R的奇函数,当x≤0时,f(x)=3x+a,则f(2)的值为( )A、
9. 已知函数f(x)是定义域为R的奇函数,当x≤0时,f(x)=3x+a,则f(2)的值为( )A、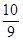 B、
B、 C、-
C、-  D、-
D、- 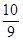 10. 某几何体的二视图如图,则该几何体的表面积为( )
10. 某几何体的二视图如图,则该几何体的表面积为( ) A、(8+4
A、(8+4 )π
B、(8+2
)π
B、(8+2  )π
C、(4+4
)π
C、(4+4  )π
D、(4+2
)π
D、(4+2  )π
11. 若函数f(x)=x3﹣mx2+4恰有两个零点,则实数m=( )A、1 B、2 C、3 D、412. 如图,在正方体ABCD﹣A1B1C1D1中,AM⊥平面A1BD,垂足为M,以下四个结论中正确的个数为( )
)π
11. 若函数f(x)=x3﹣mx2+4恰有两个零点,则实数m=( )A、1 B、2 C、3 D、412. 如图,在正方体ABCD﹣A1B1C1D1中,AM⊥平面A1BD,垂足为M,以下四个结论中正确的个数为( )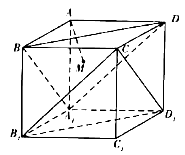
①AM垂直于平面CB1D1;②直线AM与BB1所成的角为45°;③AM的延长线过点C1;④直线AM与平面A1B1C1D1所成的角为60°
A、1 B、2 C、3 D、4二、填空题
-
13. 已知向量 ,若 ,则x=14. 若x,y满足约束条件 ,则z=2x+3y的最大值为 .15. 我国南宋著名数学家秦九韶在《数学九章》的“田域类”中写道:问沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里,…,欲知为田几何.意思是已知三角形沙田的三边长分别为13,14,15里,求三角形沙田的面积.请问此田面积为平方里.16. 已知a>0,b>0,2a+b=1,则 的最小值为 .
三、解答题
-
17. 已知数列{an}为等差数列,数列{an},{bn}满足a1=b1=2,b2=6,且an+1bn=anbn+bn+1 .(1)、求{an}的通项公式;(2)、求{bn}的前n项和Sn .18. 已知函数f(x)=asin2x﹣2cos2x+1(a∈R)的图象经过点(﹣ ,1)(1)、求a;(2)、若在区间[0,m]上存在唯一实数x0 , 使得f(x0)=2,求实数m的取值范围.19. 已知△ABC的内角A,B,C的对边分别为a,b,c,且asinB=bsin(A+ ).(1)、求A;(2)、若b, a,c成等差数列,△ABC的面积为2 ,求a.20. 如图,在三棱柱ABC﹣A1B1C1中,点D是A1B的中点,点E是B1C1的中点.
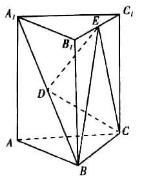 (1)、求证:DE∥平面ACC1A1;(2)、若△ABC的面积为 ,三棱柱ABC﹣A1B1C1的高为3,求三棱锥D﹣BCE的体积.
(1)、求证:DE∥平面ACC1A1;(2)、若△ABC的面积为 ,三棱柱ABC﹣A1B1C1的高为3,求三棱锥D﹣BCE的体积.