山东省菏泽市2018-2019学年高一上学期数学考试试卷
试卷更新日期:2019-01-05 类型:期中考试
一、单选题
-
1. 设集合 , ,若 且 ,则 等于( )A、2 B、3 C、4 D、62. 函数 的定义域为A、
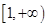 B、
B、 C、
C、 D、
D、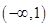 3. 下列四组函数中表示同一函数的是( )A、
3. 下列四组函数中表示同一函数的是( )A、 ,
,  B、
B、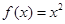 ,
, 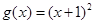 C、
C、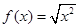 ,
, 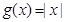 D、
D、 ,
,  4. 函数 对任意的实数 都有 ,则( )A、
4. 函数 对任意的实数 都有 ,则( )A、 B、
B、 C、
C、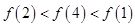 D、
D、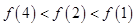 5. 已知函数 ,若 ,则实数a等于A、4 B、0 C、 D、26. 已知函数 ,则 的值为A、1 B、3 C、5 D、77. 下列函数是偶函数且在 上是减函数的是A、 B、
5. 已知函数 ,若 ,则实数a等于A、4 B、0 C、 D、26. 已知函数 ,则 的值为A、1 B、3 C、5 D、77. 下列函数是偶函数且在 上是减函数的是A、 B、 C、
D、
C、
D、 8. 已知 ,且 ,则 的值为A、
8. 已知 ,且 ,则 的值为A、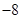 B、8
C、
B、8
C、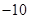 D、10
9. 已知 , ,一次函数是 ,二次函数是 ,则下列图象中可以成立的是A、
D、10
9. 已知 , ,一次函数是 ,二次函数是 ,则下列图象中可以成立的是A、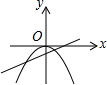 B、
B、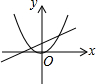 C、
C、 D、
D、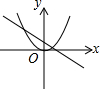 10. 若函数 的零点在区间 内,则b的取值范围为A、
10. 若函数 的零点在区间 内,则b的取值范围为A、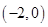 B、
B、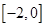 C、
C、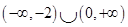 D、
D、 11. 已知奇函数
11. 已知奇函数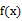 的定义域为R,且当 , 时,满足 成立,则 的x取值范围是 A、
的定义域为R,且当 , 时,满足 成立,则 的x取值范围是 A、 B、
B、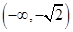 C、
C、 D、
D、 12. 已知 ,函数 ,若函数 恰有2个零点,则a的取值范围是A、
12. 已知 ,函数 ,若函数 恰有2个零点,则a的取值范围是A、 ,
,  B、
B、 C、
C、 D、
D、
二、填空题
-
13. .14. 已知集合A={m+2,2m2+m},若3∈A,则m的值为 .15. 函数 的值域是 .16. 对a, ,设 ,函数 若关于x的方程 有两个不同的实数解,则实数k的取值范围是 .
三、解答题
-
17. 已知 2,3,4,5,6, , 4, , .
求: , , , , .
18. 已知全集 ,集合 , .(1)、若 ,求 , ;(2)、若 ,求实数a的取值范围.19. 已知函数 满足 .(1)、求 ;(2)、方程 的两个不等实根为 , ,求a的取值范围及 的值 用a表示 .20. 已知函数 .(1)、在给定的直角坐标系内画出 的图象;(2)、写出 的单调区间,并指出单调性 不要求证明 ;(3)、若函数 有两个不同的零点,求实数a的取值范围.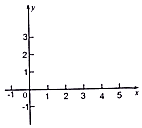 21. 某市有A、B两家羽毛球球俱乐部,两家设备和服务都很好,但收费方式不同,A俱乐部每块场地每小时收费6元;B俱乐部按月计费,一个月中20小时以内 含20小时 每块场地收费90元,超过20小时的部分,每块场地每小时2元,某企业准备下个月从这两家俱乐部中的一家租用一块场地开展活动,其活动时间不少于12小时,也不超过30小时.(1)、设在A俱乐部租一块场地开展活动x小时的收费为 元 ,在B俱乐部租一块场地开展活动x小时的收费为 元 ,试求 与 的解析式;(2)、问该企业选择哪家俱乐部比较合算,为什么?22. 已知二次函数 .(1)、若 ,求a的值;(2)、若对于任意的 , 恒成立,求实数a的取值范围.
21. 某市有A、B两家羽毛球球俱乐部,两家设备和服务都很好,但收费方式不同,A俱乐部每块场地每小时收费6元;B俱乐部按月计费,一个月中20小时以内 含20小时 每块场地收费90元,超过20小时的部分,每块场地每小时2元,某企业准备下个月从这两家俱乐部中的一家租用一块场地开展活动,其活动时间不少于12小时,也不超过30小时.(1)、设在A俱乐部租一块场地开展活动x小时的收费为 元 ,在B俱乐部租一块场地开展活动x小时的收费为 元 ,试求 与 的解析式;(2)、问该企业选择哪家俱乐部比较合算,为什么?22. 已知二次函数 .(1)、若 ,求a的值;(2)、若对于任意的 , 恒成立,求实数a的取值范围.