山东日照市2018-2019学年高三上学期理数期中考试试卷
试卷更新日期:2019-01-05 类型:期中考试
一、单选题
-
1. 集合 , ,则A、
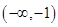 B、
B、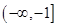 C、
C、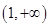 D、
D、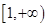 2. 命题 , ;命题 , ,则下列命题中为真命题的是( ).A、
2. 命题 , ;命题 , ,则下列命题中为真命题的是( ).A、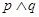 B、
B、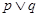 C、
C、 D、
D、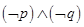 3. 已知向量 , 满足 ( )A、
3. 已知向量 , 满足 ( )A、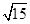 B、
B、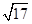 C、
C、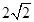 D、
4. 函数 的定义域为( )A、 B、
D、
4. 函数 的定义域为( )A、 B、 C、
C、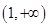 D、
D、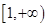 5. 将函数 的图象向左平移 个单位,所得的图象所对应的函数解析式是( )A、
5. 将函数 的图象向左平移 个单位,所得的图象所对应的函数解析式是( )A、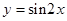 B、
B、 C、
C、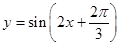 D、
D、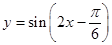 6. 已知 ,则 =( )A、 B、
6. 已知 ,则 =( )A、 B、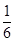 C、
D、
C、
D、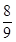 7. 已知 的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件8. 若 , , ,定义在 上的奇函数 满足:对任意的 且 都有 ,则 的大小顺序为( )A、
7. 已知 的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件8. 若 , , ,定义在 上的奇函数 满足:对任意的 且 都有 ,则 的大小顺序为( )A、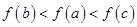 B、
B、 C、
C、 D、
D、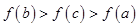 9. “中国剩余定理”又称“孙子定理”.1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法复合1801年由高斯得到的关于问余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将 到 这 个数中,能被 除余 且被 除余 的数按从小到大的顺序排成一列,构成数列 ,则此数列共有( )A、
9. “中国剩余定理”又称“孙子定理”.1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法复合1801年由高斯得到的关于问余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将 到 这 个数中,能被 除余 且被 除余 的数按从小到大的顺序排成一列,构成数列 ,则此数列共有( )A、 项
B、
项
B、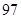 项
C、
项
C、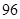 项
D、
项
D、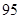 项
10. 函数 的图象大致是 ( )A、
项
10. 函数 的图象大致是 ( )A、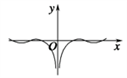 B、
B、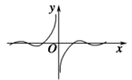 C、
C、 D、
D、 11. 已知函数 ,若函数 恰有4个零点,则实数a的取值范围为( )A、
11. 已知函数 ,若函数 恰有4个零点,则实数a的取值范围为( )A、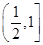 B、
B、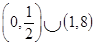 C、
C、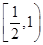 D、
D、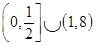 12. 已知函数 ,对x∈R恒有 ,且在区间 上有且只有一个 的最大值为( )A、
12. 已知函数 ,对x∈R恒有 ,且在区间 上有且只有一个 的最大值为( )A、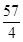 B、
B、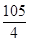 C、
C、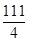 D、
D、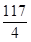
二、填空题
-
13. 已知点 ,则实数 的值为 .14. 已知实数 满足约束条件 的最小值为 .15. 学校艺术节对同一类的A,B,C,D四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是C或D作品获得一等奖”;
乙说:“B作品获得一等奖”;
丙说:“A,D两项作品未获得一等奖”;
丁说:“是C作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是 .
16. 定义在R上的奇函数 在区间 上单调递减,且 ,则不等式 的解集是 .三、解答题
-
17. 在锐角 中,角A,B,C所对的边分别为a,b,c,且满足 .(1)、求角C;(2)、若 ,求 的面积.18. 已知函数 .(1)、若函数 的图象在点 处的切线方程为 ,求 的单调区间;(2)、若函数 在 为增函数,求实数k的取值范围.19. 已知数列 是递增的等差数列, 是方程 的两根.(1)、求数列 的通项公式;(2)、求数列 的前n项和.20. 已知 .(1)、判断函数 的单调性,并证明;(2)、若函数 恰好在 上取负值,求a的值.