河南省新乡市2018-2019学年高一上学期数学期中考试试卷
试卷更新日期:2019-01-05 类型:期中考试
一、单选题
-
1. 已知集合 ,则 ( )A、{-1,2} B、{-2,-1,0,1,2} C、{1,-2} D、
 2. 已知函数 ,则 在[0,2]上的最小值为( )A、2 B、3 C、4 D、53. 函数 的定义域是( )A、
2. 已知函数 ,则 在[0,2]上的最小值为( )A、2 B、3 C、4 D、53. 函数 的定义域是( )A、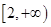 B、
B、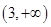 C、
C、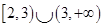 D、
D、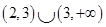 4. 已知函数 满足 ,则 ( )A、3 B、4 C、5 D、65. 下列函数为奇函数,且在定义域上是减函数的是( )A、
4. 已知函数 满足 ,则 ( )A、3 B、4 C、5 D、65. 下列函数为奇函数,且在定义域上是减函数的是( )A、 B、
B、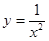 C、
C、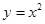 D、
D、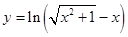 6. 已知 ,则a,b,c的大小关系是( )A、c<b<a B、a<b<c C、c<a<b D、b<c<a7. 设集合 ,则 =( )A、(0,1) B、
6. 已知 ,则a,b,c的大小关系是( )A、c<b<a B、a<b<c C、c<a<b D、b<c<a7. 设集合 ,则 =( )A、(0,1) B、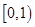 C、
D、
C、
D、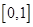 8. 已知函数 是R上的增函数,则a的取值范围为( )A、 B、
8. 已知函数 是R上的增函数,则a的取值范围为( )A、 B、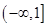 C、(0,1)
D、
9. 若函数 在(0,2)上有两个零点,则a的取值范围为( )A、(0,2) B、(0.1) C、(1,2) D、
C、(0,1)
D、
9. 若函数 在(0,2)上有两个零点,则a的取值范围为( )A、(0,2) B、(0.1) C、(1,2) D、 10. 奇函数 是R上的增函数,且 ,则不等式 的解集为( )A、
10. 奇函数 是R上的增函数,且 ,则不等式 的解集为( )A、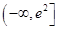 B、
B、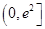 C、
C、 D、
11. 已知函数 ,若对任意 ,任意x∈R,不等式 恒成立,则k的最大值为( )A、
D、
11. 已知函数 ,若对任意 ,任意x∈R,不等式 恒成立,则k的最大值为( )A、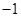 B、1
C、
D、
B、1
C、
D、
二、填空题
-
12. 函数 的零点为。13. 已知函数 是定义在R上的奇函数,则14. 某桶装水经营部每天的固定成本为420元,每桶水的进价为5元,日均销售量y(桶)与销售单价x(元)的关系式为y=-30x+450,则该桶装水经营部要使利润最大,销售单价应定为元.15. 已知函数 .若总是存在实数a,b.使得 ,则b的取值范围为。
三、解答题