河南省洛阳市、许昌市2018-2019学年高三文数第一次质量检测试卷
试卷更新日期:2019-01-05 类型:高考模拟
一、单选题
-
1. 已知全集U=R,集合M={x| <1},集合N={ y|y= },则(CUM)∩N=( )A、(1,2) B、[0,2] C、(0,2] D、[1,2]2. 若复数 满足 ,则复数 的虚部为( )A、
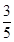 B、
B、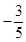 C、
C、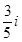 D、
D、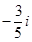 3. 已知等比数列{ }中,a3=2,a4a6=16,则 的值为( )A、2 B、2 C、
3. 已知等比数列{ }中,a3=2,a4a6=16,则 的值为( )A、2 B、2 C、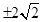 D、
D、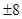 4. 祖暅原理:“幂势既同,则积不容异”,它是中国古代一个涉及几何体体积的问题,意思是两个同高的几何体,如果在等高处的截面积恒相等,那么体积相等.设A,B为两个同高的几何体,p:A,B的体积不相等,q:A,B在等高处的截面积不恒相等,根据祖暅原理可知,p是q的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 若双曲线 的一条渐近线与圆 至多有一个交点,则双曲线离心率的取值范围是( )A、
4. 祖暅原理:“幂势既同,则积不容异”,它是中国古代一个涉及几何体体积的问题,意思是两个同高的几何体,如果在等高处的截面积恒相等,那么体积相等.设A,B为两个同高的几何体,p:A,B的体积不相等,q:A,B在等高处的截面积不恒相等,根据祖暅原理可知,p是q的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 若双曲线 的一条渐近线与圆 至多有一个交点,则双曲线离心率的取值范围是( )A、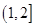 B、
B、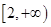 C、
C、 D、
D、 6. 已知cos(α+ )-sinα= ,则sin(α- )的值为( )A、
6. 已知cos(α+ )-sinα= ,则sin(α- )的值为( )A、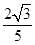 B、-
B、- 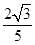 C、
D、-
7. 执行如图所示的程序框图,若输出的S= ,则判断框内填入的条件不可以是( )
C、
D、-
7. 执行如图所示的程序框图,若输出的S= ,则判断框内填入的条件不可以是( )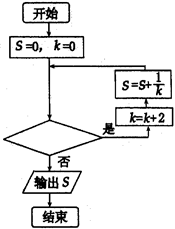 A、k≤7? B、k<7? C、k≤8? D、k<8?8. 已知实数x,y满足 则x2+y2-2x的取值范围是( )A、[0,19] B、[-
A、k≤7? B、k<7? C、k≤8? D、k<8?8. 已知实数x,y满足 则x2+y2-2x的取值范围是( )A、[0,19] B、[-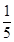 ,20]
C、[0,20]
D、[-
,20]
C、[0,20]
D、[- 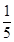 ,19]
9. 某空间几何体的三视图如图所示(图中小正方形的边长为1),则这个几何体的体积是( )
,19]
9. 某空间几何体的三视图如图所示(图中小正方形的边长为1),则这个几何体的体积是( )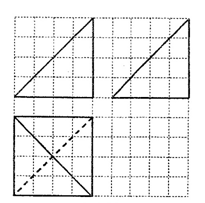 A、
A、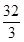 B、
B、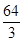 C、16
D、32
10. 已知函数f(x)=sin(ωx+θ),其中ω>0,θ∈(0, ), = =0,(x1≠x2),|x2-x1|min= ,f(x)=f( -x),将函数f(x)的图象向左平移 个单位长度得到函数g(x)的图象,则函数g(x)的单调递减区间是( )A、[kπ- ,kπ+
C、16
D、32
10. 已知函数f(x)=sin(ωx+θ),其中ω>0,θ∈(0, ), = =0,(x1≠x2),|x2-x1|min= ,f(x)=f( -x),将函数f(x)的图象向左平移 个单位长度得到函数g(x)的图象,则函数g(x)的单调递减区间是( )A、[kπ- ,kπ+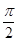 ](k∈Z)
B、[kπ,kπ+
](k∈Z)
B、[kπ,kπ+ 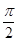 ](k∈Z)
C、[kπ+
](k∈Z)
C、[kπ+ 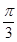 ,kπ+
,kπ+ 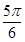 ](k∈Z)
D、[kπ+
](k∈Z)
D、[kπ+ 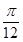 ,kπ+
,kπ+ 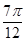 ](k∈Z)
11. 设函数 ,的导函数为 ,且 , ,则下列不等式成立的是(注:e为自然对数的底数)( )A、
](k∈Z)
11. 设函数 ,的导函数为 ,且 , ,则下列不等式成立的是(注:e为自然对数的底数)( )A、 B、
B、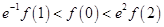 C、
C、 D、
D、 12. 已知F1 , F2分别为椭圆 (a>b>0)的左、右焦点,P为椭圆上一点,O为坐标原点,且( + )· =0,| |=2| |,则该椭圆的离心率为( )A、
12. 已知F1 , F2分别为椭圆 (a>b>0)的左、右焦点,P为椭圆上一点,O为坐标原点,且( + )· =0,| |=2| |,则该椭圆的离心率为( )A、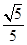 B、
B、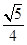 C、
C、 D、
D、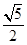 13. 平面直角坐标系中, 为原点, 三点满足 ,则 ( )A、1 B、2 C、3 D、
13. 平面直角坐标系中, 为原点, 三点满足 ,则 ( )A、1 B、2 C、3 D、二、填空题
-
14. 已知函数f(x)= ,若|f(a)|≥2,则实数a的取值范围是 .15. 在直三棱柱ABC—A1B1C1中,∠ACB=90°,AC=2,BC=CC1= ,P是BC1上一动点,则A1P+PC的最小值为 .16. 已知函数f(x)=2cosx+sin2x,则f(x)的最小值是 .
三、解答题
-
17. △ABC中,已知B=2C,AB:AC=2:3.(1)、求cosC;(2)、若AC= ,求BC的长度.18. 已知{ }是公差不为0的等差数列,其中a1=1,且a2 , a3 , a6成等比数列.(1)、求数列{ }的通项公式;(2)、记 是数列{ }的前n项和,是否存在n∈N﹡,使得 +9n+80<0成立?若存在,求n的最小值;若不存在,说明理由.19. 如图,等腰三角形PAD所在平面与菱形ABCD所在平面互相垂直,已知点E,F,M,N分别为边BA,BC,AD,AP的中点.
 (1)、求证:AC⊥PE;(2)、求证:PF∥平面BNM.20. 已知抛物线C:x2=2py(p>0)的焦点为F,抛物线上一点P的纵坐标为3,且|PF|=4,过M(m,0)作抛物线C的切线MA(斜率不为0),切点为A.(1)、求抛物线C的方程;(2)、求证:以FA为直径的圆过点M.21. 设函数f(x)=(x2-1)lnx-x2+2x.(1)、求曲线y=f(x)在点(2,f(2))处的切线方程;(2)、证明:f(x)≥1.
(1)、求证:AC⊥PE;(2)、求证:PF∥平面BNM.20. 已知抛物线C:x2=2py(p>0)的焦点为F,抛物线上一点P的纵坐标为3,且|PF|=4,过M(m,0)作抛物线C的切线MA(斜率不为0),切点为A.(1)、求抛物线C的方程;(2)、求证:以FA为直径的圆过点M.21. 设函数f(x)=(x2-1)lnx-x2+2x.(1)、求曲线y=f(x)在点(2,f(2))处的切线方程;(2)、证明:f(x)≥1.