人教版八年级数学上册 14.1 整式的乘法(5) 同步练习
试卷更新日期:2019-01-03 类型:同步测试
一、选择题
-
1. 计算:(2x2)3﹣6x3(x3+2x2+x)=( )A、﹣12x5﹣6x4 B、2x6+12x5+6x4 C、x2﹣6x﹣3 D、2x6﹣12x5﹣6x42. 计算(﹣3x)•(2x2﹣5x﹣1)的结果是( )A、﹣6x2﹣15x2﹣3x B、﹣6x3+15x2+3x C、﹣6x3+15x2 D、﹣6x3+15x2﹣13. 单项式乘以多项式运算法则的依据是( )A、乘法交换律 B、加法结合律 C、乘法分配律 D、加法交换律4. 已知A=﹣4x2 , B是多项式,在计算B+A时,小马虎同学把B+A看成了B•A,结果得32x5﹣16x4 , 则B+A为( )A、﹣8x3+4x2 B、﹣8x3+8x2 C、﹣8x3 D、8x35. 若x+y+3=0,则x(x+4y)﹣y(2x﹣y)的值为( )A、3 B、9 C、6 D、﹣96. 代数式yz(xz+2)﹣2y(3xz2+z+x)+5xyz2的值( )A、只与x,y有关 B、只与y,z有关 C、与x,y,z都无关 D、与x,y,z都有关
二、填空题
-
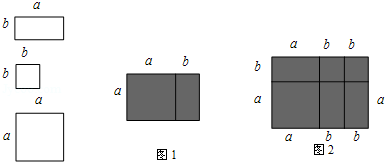
7. 今天数学课上,老师讲了单项式乘以多项式,放学回到家,小明拿出课堂笔记本复习,发现一道题:﹣3xy(4y﹣2x﹣1)=﹣12xy2+6x2y+□,□的地方被墨水弄污了,你认为□处应填写 .8. 方程2x(x﹣1)=12+x(2x﹣5)的解是 .9. 如果三角形的一边长为m2+n2 , 该边上的高为4m2n,那么这个三角形的面积为.10. 若2a+3b-6=0,则多项式6a+9b-12的值是 .11. 如图,有多个长方形和正方形的卡片,图甲是选取了2块不同的卡片,拼成的一个图形,借助图中阴影部分面积的不同表示可以用来验证等式a(a+b)=a2+ab成立,根据图乙,利用面积的不同表示方法,仿照上边的式子写出一个等式 .
三、解答题
